
【题目】关于x的一元二次方程x2+(2k+1)x+k2+1=0有两个不等实根![]() .
.
(1)求实数k的取值范围.
(2)若方程两实根![]() 满足|x1|+|x2|=x1·x2,求k的值.
满足|x1|+|x2|=x1·x2,求k的值.
【答案】(1)k﹥![]() ;(2)k=2.
;(2)k=2.
【解析】
试题:(1)根据方程有两个不相等的实数根可得△>0,代入求得k的取值范围即可;(2)首先判断出两根均小于0,然后去掉绝对值,进而得到2k+1=k2+1,结合k的取值范围解方程即可.
试题解析:(1)∵原方程有两个不相等的实数根
∴ Δ=(2k+1)2-4(k2+1)=4k2+4k+1-4k2-4=4k-3﹥0
解得:k﹥![]() ;
;
∵k﹥![]() ,
,
∴x1+x2 =-(2k+1)<0
又∵x1·x2=k2+1﹥0
∴x1<0,x2<0,
∴|x1|+|x2|=-x1-x2 =-(x1+x2)=2k+1
∵|x1|+|x2|=x1·x2
∴2k+1=k2+1,
∴k1=0,k2=2
又 ∵k﹥![]()
∴k=2.


科目:初中数学 来源: 题型:
【题目】如图,点O(0,0),A(0,1)是正方形OAA1B的两个顶点,以OA1对角线为边作正方形OA1A2B1,再以正方形的对角线OA2作正方形OA1A2B1,…,依此规律,则点A2017的坐标是( )

A. (0,21008) B. (21008,21008) C. (21009,0) D. (21009,-21009)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,学习完“代入消元法”和“加减消元法“解二元一次方程组后,善于思考的小铭在解方程组![]() 时,采用了一种“整体代换”的解法:
时,采用了一种“整体代换”的解法:
解:将方程②变形:4x+10y+y=5,即2(2x+5y)+y=5③.
把方程①代入③得:2×3+y=5,∴y=﹣1①得x=4,所以,方程组的解为![]() .
.
请你解决以下问题:
(1)模仿小铭的“整体代换”法解方程组![]() .
.
(2)已知x,y满足方程组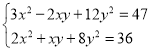 ,求x2+4y2﹣xy的值.
,求x2+4y2﹣xy的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,铁路上A,B两点相距25 km,C,D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=15 km,CB=10 km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2) 如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=![]() ,其中
,其中![]() 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,CA=CB,CD∥AB且与OA的延长线交与点D.
(1)判断CD与⊙O的位置关系并说明理由;
(2)若∠ACB=120°,OA=2,求CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了减少二氧化碳的排放量,提倡绿色出行,越来越多市民选择租用共享单车出行,已知某共享单车公司为市民提供了手机支付(使用的前1小时免费)和会员卡支付两种支付方式,如图描述了两种方式应支付金额y(元)与骑行时间x(时)之间的函数关系,根据图象回答下列问题:

(1)图中表示会员卡支付的收费方式是 (填①或②).
(2)在图①中当x≥1时,求y与x的函数关系式.
(3)陈老师经常骑行该公司的共享单车,请根据不同的骑行时间帮他确定选择哪种支付方式比较合算.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com