
【题目】如图,△ABC是等腰直角三角形,且∠C=90°,直线l过C点.

(1)如图1,过A点、B点作直线l的垂线段AD、BE,垂足为D、E,请你探究AD、BE、DE满足的数量关系,并进行证明;
(2)当直线l绕点C旋转到如图2所示的位置时,请直接写出AD、BE和DE的数量关系(不用证明)
【答案】(1)DE=AD+BE,证明见解析;(2)DE=BEAD.
【解析】试题分析:(1)证△ACD≌△CBE,由全等三角形的性质可得出DC=EB,AD=CE,再结合DE=DC+CE即可得出DE=AD+BE;(2)同理得出△ACD≌△CBE,由全等三角形的性质可得出DC=EB,AD=CE,再结合DE=DC-CE即可得出DE=BE-AD.
解:(1)DE=AD+BE,证明:
∵△ABC是等腰直角三角形,
∴AC=BC.
∵∠ACB=90°,AD⊥直线l,
∴∠ACD+∠BCE=90°,∠ACD+∠CAD=90°,
∴∠CAD=∠BCE.
在△ACD和△CBE中,∠ADC=∠CEB=90°,∠CAD=∠BCE,AC=CB,
∴△ACD≌△CBE(AAS),
∴DC=EB,AD=CE,
∴DE=DC+CE=AD+BE.
(2)DE=BEAD. 证明:
同(1)可证出△ACD≌△CBE,
∴DC=EB,AD=CE,
∴DE=DC-CE=BE-AD.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB的垂直平分线MN交AB于点E,交AC于点D,且AC=15cm,△BCD的周长等于25cm. 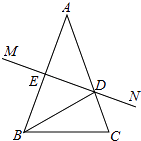
(1)求BC的长;
(2)若∠A=36°,并且AB=AC,求证:BC=BD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年春晩“奋进新时代,欢度幸福年”,在和谐、温暖、欢乐的氛围里传递了社会的正能量和浓浓的家国情怀,海内外收视的观众总规模达到11.73亿人,其中数据11.73亿用科学记数法表示正确的是( )
A. 11.73×108B. 1.173×108
C. 1.173×109D. 0.1173×1010
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,CA=CB,在△AED中, DA=DE,点D、E分别在CA、AB上.
(1)如图①,若∠ACB=∠ADE=90°,则CD与BE的数量关系是 ;
(2)若∠ACB=∠ADE=120°,将△AED绕点A旋转至如图②所示的位置,求CD与BE的数量关系;
(3)若∠ACB=∠ADE=2α(0°< α < 90°),将△AED绕点A旋转至如图③所示的位置,探究线段CD与BE的数量关系,并加以证明(用含α的式子表示).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com