
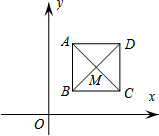
 如图,已知正方形ABCD,顶点A(1,3),B(1,1),C(3,1),对角线交于点M.规定“把正方形ABCD先沿x轴翻折,再向左平移个单位”为一次变换,那么经过两次变换后,点M的坐标变为(0,2),连续经过2015次变换后,点M的坐标变为(-2013,-2).
如图,已知正方形ABCD,顶点A(1,3),B(1,1),C(3,1),对角线交于点M.规定“把正方形ABCD先沿x轴翻折,再向左平移个单位”为一次变换,那么经过两次变换后,点M的坐标变为(0,2),连续经过2015次变换后,点M的坐标变为(-2013,-2). 分析 首先由正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1),然后根据题意求得第1次、2次、3次变换后的对角线交点M的对应点的坐标,即可得规律:第n次变换后的点M的对应点的为:当n为奇数时为(2-n,-2),当n为偶数时为(2-n,2),继而求得把正方形ABCD连续经过2014次这样的变换得到正方形ABCD的对角线交点M的坐标.
解答 解:∵正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1).
∴对角线交点M的坐标为(2,2),
根据题意得:第1次变换后的点M的对应点的坐标为(2-1,-2),即(1,-2),
第2次变换后的点M的对应点的坐标为:(2-2,2),即(0,2),
第3次变换后的点M的对应点的坐标为(2-3,-2),即(-1,-2),
第n次变换后的点M的对应点的为:当n为奇数时为(2-n,-2),当n为偶数时为(2-n,2),
∴连续经过2015次变换后,正方形ABCD的对角线交点M的坐标变为(-2013,-2).
故答案为:(0,2),(-2013,-2).,
点评 此题考查了点的坐标变化规律,对称与平移的性质.注意得到规律:第n次变换后的对角线交点M的对应点的坐标为:当n为奇数时为(2-n,-2),当n为偶数时为(2-n,2)是解此题的关键.


 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
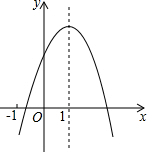 已知二次函数y=ax2+bx+c的图象如图所示,下列结论中,正确的结论的个数( )
已知二次函数y=ax2+bx+c的图象如图所示,下列结论中,正确的结论的个数( )| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
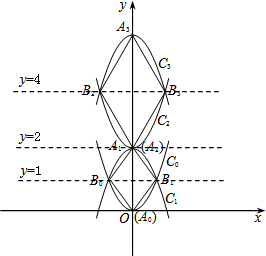 如图,已知抛物线C0:y=x2,顶点记作A0.首先我们将抛物线C0关于直线y=1对称翻折过去得到抛物线C1称为第一次操作,再将抛物线C1关于直线y=2对称翻折过去得到抛物线C2称为第二次操作,…,将抛物线Cn-1关于直线y=2n-1对称翻折过去得到抛物线Cn(顶点记作An)称为第n此操作(n=1,2,3…),….设抛物线C0与抛物线C1交于两点B0与B1,顺次连接A0、B0、A1、B1四个点得到四边形A0B0A1B1,抛物线C2与抛物线C3交于两点B2与B3,顺次连接A2、B2、A3、B3四个点得到四边形A2B2A3B3,…,抛物线Ck-1与抛物线Ck交于两点Bk-1与Bk,顺次连接Ak-1、Bk-1、Ak、Bk四个点得到四边形Ak-1Bk-1AkBk(k=1,3,5…),….
如图,已知抛物线C0:y=x2,顶点记作A0.首先我们将抛物线C0关于直线y=1对称翻折过去得到抛物线C1称为第一次操作,再将抛物线C1关于直线y=2对称翻折过去得到抛物线C2称为第二次操作,…,将抛物线Cn-1关于直线y=2n-1对称翻折过去得到抛物线Cn(顶点记作An)称为第n此操作(n=1,2,3…),….设抛物线C0与抛物线C1交于两点B0与B1,顺次连接A0、B0、A1、B1四个点得到四边形A0B0A1B1,抛物线C2与抛物线C3交于两点B2与B3,顺次连接A2、B2、A3、B3四个点得到四边形A2B2A3B3,…,抛物线Ck-1与抛物线Ck交于两点Bk-1与Bk,顺次连接Ak-1、Bk-1、Ak、Bk四个点得到四边形Ak-1Bk-1AkBk(k=1,3,5…),….查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,AB>BC>AC,小华依下列方法作图,①作∠C的角平分线交AB于点D;②作CD的中垂线,分别交AC,BC于点E,F;③连接DE,DF.根据小华所作的图,下列说法中一定正确的是( )
如图,在△ABC中,AB>BC>AC,小华依下列方法作图,①作∠C的角平分线交AB于点D;②作CD的中垂线,分别交AC,BC于点E,F;③连接DE,DF.根据小华所作的图,下列说法中一定正确的是( )| A. | 四边形CEDF为菱形 | B. | DE=DA | ||
| C. | DF⊥CB | D. | CD=BD |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com