
����Ŀ����֪��AOB��100������COD��40����OE��OF�ֱ�ƽ�֡�AOD����BOD.
(1)��ͼ1����OA��OC�غ�ʱ�����EOF�Ķ�����
(2)������COD�Ĵ�ͼ1��λ���Ƶ�O˳ʱ����ת����ת�ǡ�AOC��������0��������90��.
����ͼ2�����жϡ�BOF���COE֮�������������ϵ��˵������.
���ڡ�COD��ת�����У���ֱ��д����BOE����COF����AOC֮���������ϵ.
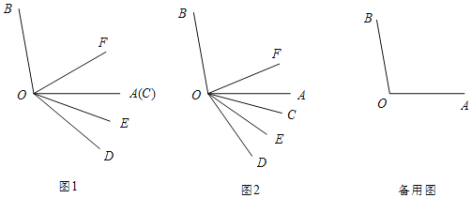
���𰸡�(1)��EOF=50����(2)�١�BOF+��COE��90�������ɼ��������ڡ�COF+��AOC����BOE��30��.
��������
(1)������ó���AOD����COD��40������BOD����AOB+��COD��140�����ɽ�ƽ���߶���ó���EOD��![]() ��AOD��20������DOF��
��AOD��20������DOF��![]() ��BOD��70�������ɵó��𰸣�
��BOD��70�������ɵó��𰸣�
(2)���ɽ�ƽ���߶���ó���EOD����AOE��![]() ��AOD��20��+
��AOD��20��+![]() ������BOF��
������BOF��![]() ��BOD��70��+
��BOD��70��+![]() ���������COE����AOE����AOC��20����
���������COE����AOE����AOC��20����![]() �������ɵó��𰸣�
�������ɵó��𰸣�
����������EOD����AOE��20��+![]() ������DOF����BOF��70��+
������DOF����BOF��70��+![]() ����
����
����AOC��40��ʱ�������COF����DOF����COD��30��+![]() ������BOE����BOD����EOD����AOB+��COD+������EOD��120��+
������BOE����BOD����EOD����AOB+��COD+������EOD��120��+![]() �������ɵó��𰸣�
�������ɵó��𰸣�
��40������AOC��90��ʱ�������COF����DOF+��DOC��150����![]() ������BOE����BOD����DOE��120��+
������BOE����BOD����DOE��120��+![]() �����ɵó���.
�����ɵó���.
�⣺(1)��OA��OC�غϣ�
���AOD����COD��40������BOD����AOB+��COD��100��+40����140����
��OEƽ����AOD��OFƽ����BOD��
���EOD��![]() ��AOD��
��AOD��![]() ��40����20������DOF��
��40����20������DOF��![]() ��BOD��
��BOD��![]() ��140����70����
��140����70����
���EOF����DOF����EOD��70����20����50����
(2)�١�BOF+��COE��90�����������£�
��OEƽ����AOD��OFƽ����BOD��
���EOD����AOE��![]() ��AOD��
��AOD��![]() (40��+��)��20��+
(40��+��)��20��+![]() ������BOF��
������BOF��![]() ��BOD��
��BOD��![]() (��AOB+��COD+��)��
(��AOB+��COD+��)��![]() (100��+40��+��)��70��+
(100��+40��+��)��70��+![]() ����
����
���COE����AOE����AOC��20��+![]() ��������20����
��������20����![]() ����
����
���BOF+��COE��70��+![]() ��+20����
��+20����![]() ����90����
����90����
���������EOD����AOE��20��+![]() ������DOF����BOF��70��+
������DOF����BOF��70��+![]() ����
����
����AOC��40��ʱ����ͼ2��ʾ��
��COF����DOF����COD��70��+![]() ����40����30��+
����40����30��+![]() ����
����
��BOE����BOD����EOD����AOB+��COD+������EOD��100��+40��+����(20��+![]() ��)��120��+
��)��120��+![]() ����
����
���BOE+��COF����AOC��120��+![]() ��+30��+
��+30��+![]() ��������150����
��������150����
��40������AOC��90��ʱ����ͼ3��ʾ��
��COF����DOF+��DOC��![]() (360����140������)+40����150����
(360����140������)+40����150����![]() ����
����
��BOE����BOD����DOE��140��+����(20��+![]() ��)��120��+
��)��120��+![]() ��
��
���COF+��AOC����BOE��150����![]() +����(120��+
+����(120��+![]() )��30����
)��30����
������������BOE����COF����AOC֮���������ϵΪ��BOE+��COF����AOC��150������COF+��AOC����BOE��30��.




 53���ò�ϵ�д�
53���ò�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�������Ʊ�۸������
��Ʊ����/�� | 1��50 | 51��100 | 100���� |
ÿ����Ʊ��/Ԫ | 12 | 10 | 8 |
ijУ���꼶��1������2������ƻ�ȥ�����þ��㣬���У�1������������50�ˣ���2������������50��������100�ˣ���������Ϊ��λ������Ʊ����һ��֧��1118Ԫ�������������������Ϊһ�����幺Ʊ����ֻ�軨��816Ԫ��
��1����������ж�����ѧ����
��2�����幺Ʊ�뵥����Ʊ��Ƚϣ����������Լ�˶���Ǯ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ı߳���4����DAC��ƽ���߽�DC�ڵ�E������P��Q�ֱ���AD��AE�ϵĶ��㣬��DQ+PQ����Сֵ��������
 A��2
A��2
B��4
C��![]()
D��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���۲����ᣬ��ش�:
![]()
(1)��![]() ���
���![]() �ľ���Ϊ ����
�ľ���Ϊ ����![]() ���
���![]() �ľ���Ϊ ��
�ľ���Ϊ ��
��![]() ���
���![]() �ľ���Ϊ ����
�ľ���Ϊ ����![]() ���
���![]() �ľ���Ϊ ��
�ľ���Ϊ ��
(2)����:�������ϣ������![]() ���
���![]() �ֱ��ʾ��
�ֱ��ʾ��![]() ��������֮��ľ���ɱ�ʾΪ
��������֮��ľ���ɱ�ʾΪ![]() (��
(��![]() ��ʾ)��
��ʾ)��
(3)���÷��ֵĽ��ۣ�����˼ά�����������:
�������ϱ�ʾ![]() �ĵ�
�ĵ�![]() ��
��![]() ֮��ľ�����
֮��ľ�����![]() ����
����![]() ��ֵ�� ��
��ֵ�� ��
��![]() ����
����![]() ��
��
���������Ƿ���ڱ�ʾ![]() �ĵ�
�ĵ�![]() ��ʹ��
��ʹ��![]() ����
����![]() ����
����![]() �ľ���֮��Ϊ
�ľ���֮��Ϊ![]() �������ڣ������
�������ڣ������![]() ��ֵ���������ڣ�˵������;
��ֵ���������ڣ�˵������;
��![]() ����СֵΪ ��
����СֵΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�һ�κ���y=kx+b��ͼ���뷴��������y=![]() ��ͼ���ཻ�ڵ�A��m��3����B����6��n������x�ύ�ڵ�C��
��ͼ���ཻ�ڵ�A��m��3����B����6��n������x�ύ�ڵ�C��
��1����һ�κ���y=kx+b�Ĺ�ϵʽ��
��2�����ͼ��ֱ��д������kx+b��![]()
![]() ��x��ȡֵ��Χ��
��x��ȡֵ��Χ��
��3������P��x���ϣ���S��ACP=![]() S��BOC�����P�����꣮
S��BOC�����P�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijũ���а���ɽ����Ķ���ֹ���2000�ã�����ˮ���ܲ���Ϊ18000ǧ�ˣ���ˮ�����г���ÿǧ����![]() Ԫ���ڹ�ÿǧ����
Ԫ���ڹ�ÿǧ����![]() Ԫ
Ԫ![]() ����ũ����ˮ�������г�����ƽ��ÿ�����1000ǧ�ˣ���8�˰�æ��ÿ��ÿ�츶����25Ԫ��ũ�ó��˷Ѽ���������˰��ƽ��ÿ��100Ԫ��
����ũ����ˮ�������г�����ƽ��ÿ�����1000ǧ�ˣ���8�˰�æ��ÿ��ÿ�츶����25Ԫ��ũ�ó��˷Ѽ���������˰��ƽ��ÿ��100Ԫ��
��1���ֱ���![]() ��ʾ���ַ�ʽ����ˮ�������룮
��ʾ���ַ�ʽ����ˮ�������룮
��2����![]() Ԫ��
Ԫ��![]() Ԫ�������ַ�ʽ������ͬ��ʱ��������ȫ��ˮ��������ͨ������˵��ѡ�����ֳ��۷�ʽ�Ϻã�
Ԫ�������ַ�ʽ������ͬ��ʱ��������ȫ��ˮ��������ͨ������˵��ѡ�����ֳ��۷�ʽ�Ϻã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
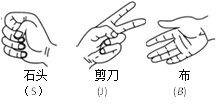
����Ŀ��С����С����������ʯͷ����������������Ϸ����Ϸ����Ϊ��ʯͷʤ����������ʤ������ʤʯͷ����ͬ��ʤ����
��1�������б�������״ͼ��ʾ�����п��ܳ��ֵ���Ϸ�����
��2����С����ʤ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ǰ��ͬѧ���ܻ���ø��ַ�ʽ���⿼��ѹ���������״̬ӭ�ӿ��ԣ�ijУ�Ը�У���꼶�IJ���ͬѧ����һ������Ϊ�����ʺ��Լ��Ŀ�ǰ��ѹ��ʽ���ĵ�����ѧУ����ѹ��ʽ��Ϊ���࣬ͬѧ�ǿɸ����Լ��������ѡ��ֻѡ����һ�࣮�����ռ�����������ͼ1��ͼ2������������ͳ��ͼ�������ͳ��ͼ�е���Ϣ����������⣺
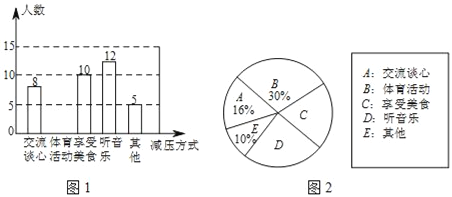
��1����ͨ�����㣬��ȫ����ͳ��ͼ��
��2����ֱ��д������ͳ��ͼ�С�������ʳ������ӦԲ�ĽǵĶ���Ϊ������
��3�����ݵ��������ɹ��Ƴ���У���꼶ѧ���м�ѹ��ʽ����������λ���ֱ���������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�ң���ABC�͡�ADE���й�������ĵ���ֱ�������Σ���BAC=��DAE=90������PΪ����BD��CE�Ľ��㣮
��1����ͼ�ף�����ADE�Ƶ�A ��ת����C��D��E��ͬһ��ֱ����ʱ������BD��BE�������и������ĸ������У�������ȷ����_____��
��BD=CE��BD��CE�ۡ�ACE+��DBC=45����BE2=2��AD2+AB2��
��2����AB=4��AD=2���ѡ�ADE�Ƶ�A��ת��
�ٵ���EAC=90��ʱ����PB�ij���
������ת�������߶�PB�������ֵ��
 ����
���� ������
������

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com