
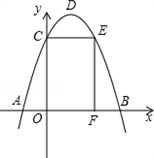
如图,抛物线y=![]() x2+mx+n交x轴于A、B两点,直线y=kx+b经过点A,与这条抛物线的对称轴交于点M(1,2),且点M与抛物线的顶点N关于x轴对称.
x2+mx+n交x轴于A、B两点,直线y=kx+b经过点A,与这条抛物线的对称轴交于点M(1,2),且点M与抛物线的顶点N关于x轴对称.
(1)求这条抛物线的函数关系式;
(2![]() )设题中的抛物线与直线的另一交点为C,已知P为线段A
)设题中的抛物线与直线的另一交点为C,已知P为线段A![]() C上一点(不含端点),过点P作PQ⊥x轴,交抛物线于点Q,试证明:当P为AC的中点时,线段PQ的长取得最大值,并求出PQ的最大值;
C上一点(不含端点),过点P作PQ⊥x轴,交抛物线于点Q,试证明:当P为AC的中点时,线段PQ的长取得最大值,并求出PQ的最大值;
(3)设D、E为直线AC上的两点(不与A、C重合),且D在E的左侧,DE=2![]() ,过点D作DF⊥x轴交抛物线于点F,过点E作EG⊥x轴交抛物线于点G.问:是否存在这样的点D,使得以D、E、F、G为顶点的四边形为平行四边形?若存在,请求出所有符合条件的点D的坐标;若不存在,请说明理由.
,过点D作DF⊥x轴交抛物线于点F,过点E作EG⊥x轴交抛物线于点G.问:是否存在这样的点D,使得以D、E、F、G为顶点的四边形为平行四边形?若存在,请求出所有符合条件的点D的坐标;若不存在,请说明理由.

(1)由题意知,抛物线顶点N的坐标为(1,-2)
∴ 其函数关系式为y=![]() (x-1)
(x-1)![]() -2=
-2=![]() x
x![]() -x-
-x-![]() .
.
(2)由 ![]() x
x![]() -x-
-x-![]() =0得 x=-1或3,即A(-1,0)、B(3,0)
=0得 x=-1或3,即A(-1,0)、B(3,0)
由A(-1,0)、M(1,2)可得直线AC的函数关系式为y=x+1.
设P(t,t+1),则Q的坐标为(x,![]() t
t![]() -t-
-t-![]() )
)
∴ PQ=(t+1)-(![]() t
t![]() -t-
-t-![]() )=-
)=-![]() t
t![]() +2t+
+2t+![]() =-
=-![]() (t-2)
(t-2)![]() +
+![]()
∴ 当t=2时,PQ有最大值为![]() ,
,
即P点运动至AC的中点时,PQ长有最大值为![]() .
.
(3)符合条件的点共有3个,分别为D1(2,3),D2( 1-2![]() ,2-2
,2-2![]() ),D3(1+2
),D3(1+2![]() ,2+2
,2+2![]() ).
).
(第(3)小题得出1解得2分,2解得3分,3解得4分)


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案科目:初中数学 来源:江苏中考真题 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2013年浙江省金华市六校联谊中考模拟数学试卷(带解析) 题型:填空题
如图,抛物线y=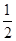 x2-
x2- x与x轴交于O,A两点. 半径为1的动圆(⊙P),圆心从O点出发沿抛物线向靠近点A的方向移动;半径为2的动圆(⊙Q),圆心从A点出发沿抛物线向靠近点O的方向移动. 两圆同时出发,且移动速度相等,当运动到P,Q两点重合时同时停止运动. 设点P的横坐标为t .
x与x轴交于O,A两点. 半径为1的动圆(⊙P),圆心从O点出发沿抛物线向靠近点A的方向移动;半径为2的动圆(⊙Q),圆心从A点出发沿抛物线向靠近点O的方向移动. 两圆同时出发,且移动速度相等,当运动到P,Q两点重合时同时停止运动. 设点P的横坐标为t .
(1)点Q的横坐标是 (用含t的代数式表示);
(2)若⊙P与⊙Q 相离,则t的取值范围是 .
查看答案和解析>>
科目:初中数学 来源:2013年浙江省金华市六校联谊中考模拟数学试卷(解析版) 题型:填空题
如图,抛物线y=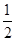 x2-
x2-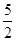 x与x轴交于O,A两点. 半径为1的动圆(⊙P),圆心从O点出发沿抛物线向靠近点A的方向移动;半径为2的动圆(⊙Q),圆心从A点出发沿抛物线向靠近点O的方向移动. 两圆同时出发,且移动速度相等,当运动到P,Q两点重合时同时停止运动. 设点P的横坐标为t .
x与x轴交于O,A两点. 半径为1的动圆(⊙P),圆心从O点出发沿抛物线向靠近点A的方向移动;半径为2的动圆(⊙Q),圆心从A点出发沿抛物线向靠近点O的方向移动. 两圆同时出发,且移动速度相等,当运动到P,Q两点重合时同时停止运动. 设点P的横坐标为t .
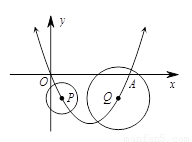
(1)点Q的横坐标是 (用含t的代数式表示);
(2)若⊙P与⊙Q 相离,则t的取值范围是 .
查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏省仪征市九年级上学期末考试数学试卷(解析版) 题型:解答题
如图,抛物线y=x2+bx+c与x轴交于点A、B(点A在点B左侧),与y轴交于点C(0,-3),且抛物线的对称轴是直线x=1.

(1)求b的值;
(2)点E是y轴上一动点,CE的垂直平分线交y轴于点F,交抛物线于P、Q两点,且点P在第三象限.当线段PQ = 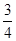 AB时,求点E的坐标;
AB时,求点E的坐标;
(3)若点M在射线CA上运动,过点M作MN⊥y轴,垂足为N,以M为圆心,MN为半径作⊙M,当⊙M与x轴相切时,求⊙M的半径.
查看答案和解析>>
科目:初中数学 来源:2012届江苏省苏州工业园区九年级上学期期中测试数学卷 题型:选择题
如图,抛物线y=x2+1与双曲线y=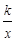 的交点A的横坐标是1,则关于x的不等式
的交点A的横坐标是1,则关于x的不等式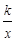 +x2+1 < 0的解集是( ▲ )
+x2+1 < 0的解集是( ▲ )
A.x>1 B.x<−1 C.0<x<1 D.−1<x<0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com