
【题目】如图①,在长方形![]() 中,
中,![]() 。点
。点![]() 从
从![]() 出发,沿
出发,沿![]() 路线运动,到
路线运动,到![]() 停止;点
停止;点![]() 出发时的速度为每秒
出发时的速度为每秒![]() ,7秒时点
,7秒时点![]() 的速度变为每秒
的速度变为每秒![]() ,图②是点
,图②是点![]() 出发
出发![]() 秒后,
秒后,![]() 的面积
的面积![]() 与
与![]() (秒)的关系图象;
(秒)的关系图象;

(1)根据题目提供的信息,求出![]() 的值为______________、
的值为______________、![]() 的值为_________
的值为_________![]() 的值为___________;
的值为___________;
(2)设点![]() 离开点
离开点![]() 的路程为
的路程为![]() ,
,
①7.5秒时,![]() 的值为_____________________;
的值为_____________________;
②请求出当动点![]() 改变速度后,
改变速度后,![]() 与
与![]() 的关系式;
的关系式;
(3)点![]() 出发后几秒,
出发后几秒,![]() 的面积
的面积![]() 是长方形
是长方形![]() 面积的
面积的![]() ?并说明理由。
?并说明理由。
【答案】(1)![]() 的值为28,
的值为28,![]() 的值为3,
的值为3,![]() 的值为14;(2)①8.5 ; ②
的值为14;(2)①8.5 ; ② ;(3)
;(3)![]() 或
或![]()
【解析】
(1)根据三角形的面积公式可求a、b及图②中c的值;
(2)①根据“速度变化前的路程+速度变化后的路程”求解即可;
②确定y与x的等量关系后列出关系式即可;
(3)①P在AB上运动时,S△APD=![]() AD×AP,AP为运动时间t的一次函数;
AD×AP,AP为运动时间t的一次函数;
②P在BC上运动时S△APD=![]() AD×AB为定值.
AD×AB为定值.
③P在DC段上运动时,S△APD=![]() AD×DP.DP为P点运动时间的一次函数.
AD×DP.DP为P点运动时间的一次函数.
先计算△APD的面积,然后将计算出来的数值代入所求函数的不同分段,解出对应的x的值,若解出的x值在对应的分段区间内,则x的值即为所求的解,反之则不是.
(1)根据图象可知S△APD=![]() AD×AP=
AD×AP=![]() ×8×(1×7)=28
×8×(1×7)=28
∴a=28;
∵AP=7,也就是P在AB上移动到了7cm,所剩部分为3cm,
当x=8时,S为40,且面积不发生变化,即P点到B点用了1秒,距离是3cm.
∴b=3cm/s,
c=18÷3+7+1=14s
(2)①∵7.5>7
∴y的值为:7×1+(7.5-7)×3=8.5cm;
②分三部分:i)运动时间从7秒到8时,
∵a=28,b=3,
∴设动点P改变速度后y与出发后的运动时间x(秒)的函数关系式为:y=kx+b,
把(7,28),(8,40)分别代入解析式得,
![]() ,
,
解得,![]()
∴y与x之间的函数关系式为:y=12x-56;
ii)运动时间从8秒到10![]() 秒时,y=40,
秒时,y=40,
iii)运动时间从10![]() 秒到14秒时,设y与x(秒)的函数关系式为:y=mx+n,
秒到14秒时,设y与x(秒)的函数关系式为:y=mx+n,
把(10![]() ,40),(14,0)代入得,
,40),(14,0)代入得,

解得,![]()
∴y与x(秒)的函数关系式为:y=-12x+168,
∴y与x(秒)的函数关系式为 ;
;
(3)S△APD=![]() s四边形ABCD=
s四边形ABCD=![]() AD×AB=16,
AD×AB=16,
①当0≤x≤7时
AP=x(cm)
S△APD=![]() AD×AP=4x
AD×AP=4x
∴4x=16,
解得,x=4
②当7<x≤8时
AP=7+(x-7)×3=3x-14
S△APD=![]() AD×AP=
AD×AP=![]() x-7
x-7
∴![]() x-7=16
x-7=16
解得,x=![]() (不符合题意,舍去)
(不符合题意,舍去)
③当P从B点运动到C点时
S△APD=![]() AD×AB=40≠16;
AD×AB=40≠16;
④当10![]() <x≤14时
<x≤14时
S△APD=-12x+168=16,
解得,x=![]() .
.
所以点P出发后4秒或![]() 秒,△APD的面积S1是长方形ABCD面积的
秒,△APD的面积S1是长方形ABCD面积的![]() .
.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,在四边形ABCD中,BD是一条对角线,∠DBC=30°,∠DBA=45°,∠C=70°.若DC=a,AB=b, 请写出求tan∠ADB的思路.(不用写出计算结果)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线过A(-1,0)、B(3,0)、C(0,-1)三点.
(1)求该抛物线的表达式;
(2)若该抛物线的顶点为D,求直线AD的解析式;
(3)点Q在y轴上,点P在抛物线上,要使Q、P、A、B为顶点的四边形是平行四边形,求所有满足条件的点标.P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
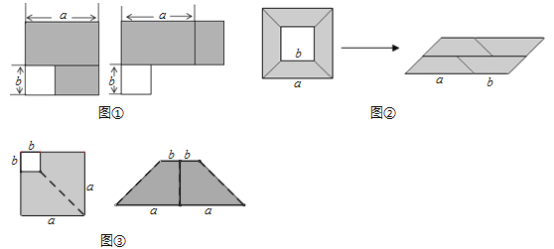
【题目】如图,阴影部分是边长是![]() 的大正方形剪去一个边长是
的大正方形剪去一个边长是![]() 的小正方形后所得到的图形,将阴影部分通过割、拼,形成新的图形,给出下列3幅图割拼方法中,其中能够验证平方差公式有___________(填序号)
的小正方形后所得到的图形,将阴影部分通过割、拼,形成新的图形,给出下列3幅图割拼方法中,其中能够验证平方差公式有___________(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC,BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.

(1)求证:四边形ABCD是矩形;
(2)若∠ADF:∠FDC=3:2,DF⊥AC,求∠BDF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 交
交![]() 轴于点
轴于点![]() 、点
、点![]() ,交
,交![]() 轴于点C,且S△ABC=6.
轴于点C,且S△ABC=6.
(1)求![]() 两点的坐标;
两点的坐标;
(2)求△ABC的外接圆与抛物线的对称轴的交点坐标;
(3)点E为抛物线上的一动点(点![]() 异于
异于![]() ,且
,且![]() 在对称轴右侧),直线
在对称轴右侧),直线![]() 交对称轴于N,
交对称轴于N,
直线BE交对称轴于![]() ,对称轴交
,对称轴交![]() 轴于
轴于![]() ,试确定
,试确定![]() 、
、![]() 的数量关系并说明理由.
的数量关系并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小正方形的边长都是1.

(1)在方格纸中画△ABC,使AB=![]() ,AC=
,AC=![]() ,BC=4;
,BC=4;
(2)请你用所学的知识验证所画的△ABC是不是直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,ABCD中,点E,F在直线AC上(点E在F左侧),BE∥DF.

(1)求证:四边形BEDF是平行四边形;
(2)若AB⊥AC,AB=4,BC=![]() ,当四边形BEDF为矩形时,求线段AE的长.
,当四边形BEDF为矩形时,求线段AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com