
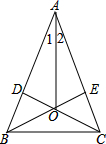
 已知:如图,CD⊥AB于D,BE⊥AC于E,CD、BE交于O,∠1=∠2.求证:OB=OC.
已知:如图,CD⊥AB于D,BE⊥AC于E,CD、BE交于O,∠1=∠2.求证:OB=OC.科目:初中数学 来源: 题型:
 在梯形ABCD中,AB∥CD,AB=a,CD=b,两腰延长线交于点M,过M作DC的平行线,分别交AC、BD延长线于E,F,则EF等于( )
在梯形ABCD中,AB∥CD,AB=a,CD=b,两腰延长线交于点M,过M作DC的平行线,分别交AC、BD延长线于E,F,则EF等于( )A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 在六一儿童节来临之际,某妇女儿童用品商场为吸引顾客,设立了一个可以自由转动的转盘(如图,转盘被平均分成20份),并规定:顾客每购物满100元,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得80元、50元、20元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可直接获得5元的购物券.转转盘和直接获得购物券,你认为哪种方式对顾客更合算?请说明理由.
在六一儿童节来临之际,某妇女儿童用品商场为吸引顾客,设立了一个可以自由转动的转盘(如图,转盘被平均分成20份),并规定:顾客每购物满100元,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得80元、50元、20元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可直接获得5元的购物券.转转盘和直接获得购物券,你认为哪种方式对顾客更合算?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com