
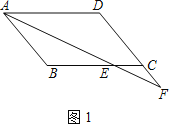
【题目】在ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F.
(1)在图1中证明CE=CF;
(2)若∠ABC=90°,G是EF的中点(如图2),直接写出∠BDG的度数;
(3)若∠ABC=120°,FG∥CE,FG=CE,分别连接DB、DG(如图3),求∠BDG的度数.
【答案】(1)见解析;(2)45°;(3)见解析.
【解析】
(1)根据AF平分∠BAD,可得∠BAF=∠DAF,利用四边形ABCD是平行四边形,求证∠CEF=∠F即可;(2)根据∠ABC=90°,G是EF的中点可直接求得;(3)分别连接GB、GC,求证四边形CEGF是平行四边形,再求证△ECG是等边三角形,由AD∥BC及AF平分∠BAD可得∠BAE=∠AEB,求证△BEG≌△DCG,然后即可求得答案.
(1)证明:如图1,
∵AF平分∠BAD,
∴∠BAF=∠DAF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠DAF=∠CEF,∠BAF=∠F,
∴∠CEF=∠F.
∴CE=CF.
(2)解:连接GC、BG,
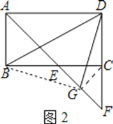
∵四边形ABCD为平行四边形,∠ABC=90°,
∴四边形ABCD为矩形,
∵AF平分∠BAD,
∴∠DAF=∠BAF=45°,
∵∠DCB=90°,DF∥AB,
∴∠DFA=45°,∠ECF=90°
∴△ECF为等腰直角三角形,
∵G为EF中点,
∴EG=CG=FG,CG⊥EF,
∵△ABE为等腰直角三角形,AB=DC,
∴BE=DC,
∵∠CEF=∠GCF=45°,
∴∠BEG=∠DCG=135°
在△BEG与△DCG中,
∵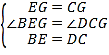 ,
,
∴△BEG≌△DCG,
∴BG=DG,
∵CG⊥EF,
∴∠DGC+∠DGA=90°,
又∵∠DGC=∠BGA,
∴∠BGA+∠DGA=90°,
∴△DGB为等腰直角三角形,
∴∠BDG=45°.
(3)解:延长AB、FG交于H,连接HD.
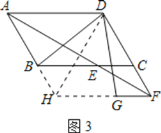
∵AD∥GF,AB∥DF,
∴四边形AHFD为平行四边形
∵∠ABC=120°,AF平分∠BAD
∴∠DAF=30°,∠ADC=120°,∠DFA=30°
∴△DAF为等腰三角形
∴AD=DF,
∴CE=CF,
∴平行四边形AHFD为菱形
∴△ADH,△DHF为全等的等边三角形
∴DH=DF,∠BHD=∠GFD=60°
∵FG=CE,CE=CF,CF=BH,
∴BH=GF
在△BHD与△GFD中,
∵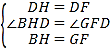 ,
,
∴△BHD≌△GFD,
∴∠BDH=∠GDF
∴∠BDG=∠BDH+∠HDG=∠GDF+∠HDG=60°.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,将△ACE沿着AE折叠以后C点正好落在AB边上的点D处.
(1)当∠B=28°时,求∠AEC的度数;
(2)当AC=6,AB=10时,
①求线段BC的长;
②求线段DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
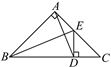
【题目】如图,△ABC是等腰直角三角形,∠BAC=90°,BE是△ABC的角平分线,ED⊥BC于点D,连接AD.
(1)请你写出图中所有的等腰三角形;
(2)若BC=10,求AB+AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与理解:
三角形中一边中点与这边所对顶点的线段称为三角形的中线。
三角形的中线的性质:三角形的中线等分三角形的面积。
即如图1,AD是![]() 中BC边上的中线,则
中BC边上的中线,则![]() ,
,
理由:![]() ,
,![]() ,
,
即:等底同高的三角形面积相等。
操作与探索:

在如图2至图4中,![]() 的面积为a。
的面积为a。
(1)如图2,延长![]() 的边BC到点D,使CD=BC,连接DA,若
的边BC到点D,使CD=BC,连接DA,若![]() 的面积为
的面积为![]() ,则
,则![]() (用含a的代数式表示);
(用含a的代数式表示);
(2)如图3,延长![]() 的边BC到点D,延长边CA到点E,使CD=BC,AE=CA,连接DE,若
的边BC到点D,延长边CA到点E,使CD=BC,AE=CA,连接DE,若![]() 的面积为
的面积为![]() ,则
,则![]() _________(用含a的代数式表示);
_________(用含a的代数式表示);
(3)在图3的基础上延长AB到点F,使BF=AB,连接FD,FE,得到![]() (如图4),若阴影部分的面积为
(如图4),若阴影部分的面积为![]() ,则
,则![]() ________(用含a的代数式表示)
________(用含a的代数式表示)
(4)拓展与应用:
如图5,已知四边形ABCD的面积是a;E,F,G,H分别是AB,BC,CD的中点,求图中阴影部分的面积?

查看答案和解析>>
科目:初中数学 来源: 题型:
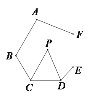
【题目】如图,在六边形ABCDEF中,∠A+∠B+∠E+∠F=α,CP、DP分别平分∠BCD、∠CDE,则∠P的度数是( )
A. ![]() α-180°B. 180°-
α-180°B. 180°-![]() C.
C. ![]() D. 360°-
D. 360°-![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米,先到终点的人原地休息.已知甲先出发2秒.在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,给出以下结论:①a=8;②b=92;③c=123.其中正确的是( )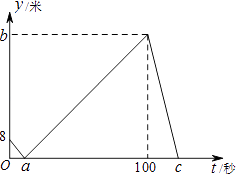
A.①②③
B.仅有①②
C.仅有①③
D.仅有②③
查看答案和解析>>
科目:初中数学 来源: 题型:
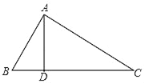
【题目】题目:如图,在△ABC中,点D是BC边上一点,连结AD,若AB=10,AC=17,BD=6,AD=8,解答下列问题:
(1)求∠ADB的度数;
(2)求BC的长.
小强做第(1)题的步骤如下:∵AB2=BD2+AD2
∴△ABD是直角三角形,∠ADB=90°.
(1)小强解答第(1)题的过程是否完整,如果不完整,请写出第(1)题完整的解答过程
(2)完成第(2)题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,AB=2,CD是边AB的高线,动点E从点A出发,以每秒1个单位的速度沿射线AC运动;同时,动点F从点C出发,以相同的速度沿射线CB运动.设E的运动时间为t(s)(t>0).
(1)AE= (用含t的代数式表示),∠BCD的大小是 度;
(2)点E在边AC上运动时,求证:△ADE≌△CDF;
(3)点E在边AC上运动时,求∠EDF的度数;
(4)连结BE,当CE=AD时,直接写出t的值和此时BE对应的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于m的方程![]() (m-16)=7的解也是关于x的方程2(x-3)-n=52的解.
(m-16)=7的解也是关于x的方程2(x-3)-n=52的解.
(1)求m,n的值;
(2)已知∠AOB=m°,在平面内画一条射线OP,恰好使得∠AOP=n∠BOP,求∠BOP.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com