
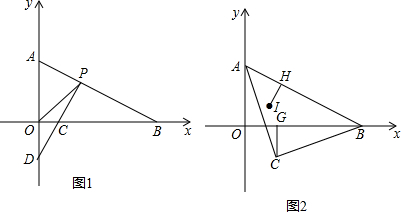
���� ��1�����ݷǸ��������ʼ��ɽ�����⣮
��2�������ֱ��AB�Ľ���ʽ�����÷����������P���꣬�����ֱ��PC�Ľ���ʽ�������C���꼴�ɽ�����⣮
��3����ͼ2�У���IE��OA��E��CM��y����M��IF��OB��F���ɡ�ACM�ա�BCF���Ƴ�AM=BG��CM=CG���Ƴ�BH-AH=OB-OA=2CG�����ɽ�����⣮
��� �⣺��1����4a2+$\frac{1}{4}$b2-16a-2b+20=0��
�ࣨ4a2-16a+16��+��$\frac{1}{4}$b2-2b+4��=0��
��4��a-2��2+$\frac{1}{4}$��b-4��2=0��
��4��a-2��2��0��$\frac{1}{4}$��b-4��2��0��
��a=2��b=4��
��A��0��2����B��4��0����
��2����ͼ1�У�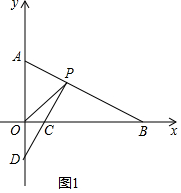
��A��0��2����B��4��0����
��ֱ��AB�Ľ���ʽΪy=-$\frac{1}{2}$x+2��
��P��m��m����
���P��ֱ��y=x�ϣ�
��$\left\{\begin{array}{l}{y=x}\\{y=-\frac{1}{2}x+2}\end{array}\right.$���$\left\{\begin{array}{l}{x=\frac{4}{3}}\\{y=\frac{4}{3}}\end{array}\right.$��
���P��$\frac{4}{3}$��$\frac{4}{3}$����
��PC��AB��
��ֱ��PC�Ľ���ʽΪy=2x-$\frac{4}{3}$��
���C������$\frac{2}{3}$��0����
��OC=$\frac{2}{3}$��BC=$\frac{10}{3}$��
��$\frac{{S}_{��BCP}}{{S}_{��OCP}}$=$\frac{\frac{2}{3}}{\frac{10}{3}}$=$\frac{1}{5}$��
��3��$\frac{BH-AH}{CG}$��ֵ���䣮�������£�
��ͼ2�У���IE��OA��E��CM��y����M��IF��OB��F��
����I�ǡ�OAB�Ľ�ƽ������OP�Ľ��㣬OPƽ�֡�AOB��
��I�����ģ���IH��AB��IE��OA��IF��OB��
��IE=IH=IF����֪AH=AE��BF=BH��
��BH-AH=BF-AE=OB-OA��
�ߡ�MCG=��ACB=90�㣬
���ACM=��BCG��
�ڡ�ACM�͡�BCG�У�
$\left\{\begin{array}{l}{��AMC=BFC}\\{��ACM=��BCF}\\{AC=BC}\end{array}\right.$��
���ACM�ա�BCF��
��AM=BG��CM=CG��
�ߡ�OMC=��OGC=��MOG=90�㣬
���ı���OMCG�Ǿ��Σ���CM=CG��
���ı���OMCG�������Σ�
��OM=OG=CG=CM��
��BH-AH=OB-AO=��BG+OG��-��AM-OM��=2CG��
��$\frac{BH-AH}{CG}$=$\frac{2CG}{CG}$=2��
���� ���⿼���������ۺ��⡢һ�κ�����ȫ�������ε��ж������ʡ����������ĵ����ʵ�֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ�����Ӹ����ߣ�����ȫ�������Σ������п�ѹ���⣮


 �п�������㾫��ϵ�д�
�п�������㾫��ϵ�д� ������ĩ��ϰ��ѵ��ϵ�д�
������ĩ��ϰ��ѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
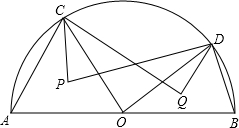 ��ͼ��֪ABΪ���O��ֱ����C��DΪ��$\widehat{AB}$�����㣬P��Q�ֱ�Ϊ��OAC����OBD�����ģ�֤����CP•CQ=DP•DQ��
��ͼ��֪ABΪ���O��ֱ����C��DΪ��$\widehat{AB}$�����㣬P��Q�ֱ�Ϊ��OAC����OBD�����ģ�֤����CP•CQ=DP•DQ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 30 | B�� | 20 | C�� | 10 | D�� | �����ܣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{3}$ | B�� | $\frac{1}{2}$ | C�� | $\frac{2}{3}$ | D�� | $\frac{3}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com