
【题目】如图,把矩形![]() 沿
沿![]() 翻折,点
翻折,点![]() 恰好落在
恰好落在![]() 边的
边的![]() 处,若
处,若![]() ,
,![]() ,则
,则![]() 的面积是( )
的面积是( )
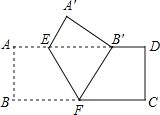
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
根据翻折的性质可得出“BF=B′F,∠BFE=∠B′FE,设AE=A′E=x,∠A′B′F=∠B=90°,∠A′=∠A=90°”,根据平行线的性质以及∠EFB=60°即可得出∠B′EF=∠B′FE=60°,进而得出△B′EF为等边三角形,在Rt△A′B′E中,结合特殊角、勾股定理求出B′E的长度,再依据等边三角形的性质以及三角形的面积公式即可得出结论.
解:∵四边形ABCD为矩形,
∴∠B=∠A=90°,AD∥BC.
由翻折的性质可知:
BF=B′F,∠BFE=∠B′FE,设AE=A′E=x,∠A′B′F=∠B=90°,∠A′=∠A=90°.
∵∠EFB=60°,AD∥BC,
∴∠B′EF=∠EFB=∠B′FE=60°,
∴△B′EF为等边三角形,
∴∠EB′F=60°.
在Rt△A′B′E中,A′E=x,∠A′=90°,∠A′B′E=∠A′B′F-∠EB′F=30°,
∴EB′=2 A′E=2x,AE+ EB′=AB′,即x+2x=9,解得x=3,所以AE=A′E=3,EB′=6,
由勾股定理得:AB=A′B′=3,所以 S△EFB′′=![]() ×6×3
×6×3![]() =9
=9![]() .
.
故选:B.


科目:初中数学 来源: 题型:
【题目】探究题:
(一)小明在玩积木时,把三个正方体积木摆成一定的形状,正面看如图①所示:

(1)若图中的△DEF为直角三角形,∠DEF=90°,正方形P的面积为9,正方形Q的面积为15,则正方形M的面积为________;
(2)若P的面积为36cm,Q的面积为64cm,同时M的面积为100cm,则△DEF为________三角形.
(二)图形变化:如图②,分别以直角三角形ABC(∠ACB=90°)的三边为直径向三角形外作三个半圆,你能找出这三个半圆的面积S1、S2、S3之间有什么关系吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,P是BC上一动点,(不与B、C重合)① CE平分∠DCF,② AP⊥PE,③ AP=EP.以此三个条件中的两个为条件,另一个为结论,可构成三个命题,即:①② ③,①③ ②,②③ ①.
(1)试判断上述三个命题是否正确(直接作答);
(2)请选择一个你认为正确的命题给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
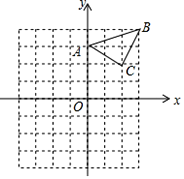
(1)△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 ;(画出图形)
(3)△A2B2C2的面积是 平方单位.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校教学楼AB的后面有一建筑物CD,在距离CD的正后方30米的观测点P处,以22°的仰角测得建筑物的顶端C恰好挡住教学楼的顶端A,而在建筑物CD上距离地面3米高的E处,测得教学楼的顶端A的仰角为45°,求教学楼AB的高度.(参考数据:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具商店销售功能相同的两种品牌的计算器,购买2个A品牌和1个B品牌的计算器共需122元;购买1个A品牌和2个B品牌的计算器共需124元.
(1)求这两种品牌计算器的单价;
(2)学校开学前夕,该商店举行促销活动,具体办法如下:购买A品牌计算器按原价的九折销售,购买B品牌计算器超出10个以上超出的部分按原价的八折销售,①设购买x个A品牌的计算器需要y1元,购买x个B品牌的计算器需要y2元,分别求出y1、y2关于x的函数关系式;
②小明准备联系一部分同学集体购买同一品牌的计算器,若购买计算器的数量超过10个,问购买哪种品牌的计算器更合算?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着交通道路的不断完善,带动了旅游业的发展,某市旅游景区有A、B、C、D、E等著名景点,该市旅游部门统计绘制出2017年“五一”长假期间旅游情况统计图,根据以下信息解答下列问题:

(1)2017年“五一”期间,该市周边景点共接待游客 万人,扇形统计图中A景点所对应的圆心角的度数是 ,并补全条形统计图.
(2)根据近几年到该市旅游人数增长趋势,预计2018年“五一”节将有80万游客选择该市旅游,请估计有多少万人会选择去E景点旅游?
(3)甲、乙两个旅行团在A、B、D三个景点中,同时选择去同一景点的概率是多少?请用画树状图或列表法加以说明,并列举所用等可能的结果.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com