Question

16．已知抛物线C：y=mx²-2mx-3m，其中m＞0，与x轴交于A、B两点（A在B左侧），与y轴交于C，且OB=OC

（1）求抛物线的解析式；
（2）如图1，若点P为对称轴右侧抛物线上一点，过A、B、P三点作⊙Q，且∠PQB=90°，求点P的坐标；
（3）如图2，将抛物线C向左平移1个单位，再向上平移$\frac{15}{4}$个单位得到新抛物线C₁，直线y=kx与抛物线C₁交于M、N两点，$\frac{1}{MO}$+$\frac{1}{NO}$是否为定值？请说明理由．

Answer 1

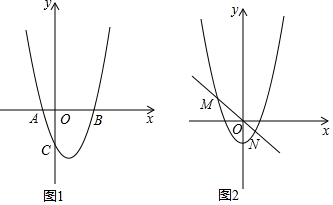
分析 （1）由解析式可求得B点坐标，再结合条件可求得m的值，可求得抛物线解析式；
（2）当点P在x轴上方时，连接AP交y轴于点S，由条件可求得OA=OC=1，可求得直线AP的解析式，联立抛物线与直线AP解析式可求得P点坐标，当点P在x轴下方时，同理可求得点P的坐标；
（3）可先求得抛物线C₁的解析式，分别设M（x₁，y₁），N（x₂，y₂），则可分别表示出MO和NO，再结合一元二次方程根与系数的关系，整理可得$\frac{1}{MO}$+$\frac{1}{NO}$为定值．

解答 解：
（1）在y=mx²-2mx-3m中，令y=0可得mx²-2mx-3m=0，解得x=-1或x=3，
∴A（-1，0），B（3，0），
∴OC=OB=3，
∴C（0，-3），即-3m=-3，解得m=1，
∴抛物线解析式为y=x²-2x-3；
（2）当P在x轴上方时，连接AP交y轴于点s，如图，

∵∠PQB=90°，
∴∠PAB=45°，
∴OA=OS=1，
∴直线AP解析式为y=x+1，
联立直线AP与抛物线解析式可得x²-2x-3=x+1，解得x=-1（舍去）或x=4，
∴P（4，5）；
当点P在x轴下方时，则直线AP解析式为y=-x-1，
联立直线AP与抛物线解析式可得x²-2x-3=-x-1，解得x=-1（舍去）或x=2，
∴P（2，-3）；
综上可知P点坐标为（4，5）或（2，-3）；
（3）为定值．
理由如下：
由平移可知抛物线C₁的解析式为y=x²-$\frac{1}{4}$，
设M（x₁，y₁），N（x₂，y₂），
∴MO²=x₁²+y₁²=y₁+$\frac{1}{4}$+y₁²=（y₁+$\frac{1}{2}$）²，
∴MO=y₁+$\frac{1}{2}$，同理NO=y₂+$\frac{1}{2}$，
∵M、N在直线y=kx上，
∴y₁=kx₁，y₂=kx₂，
∴$\frac{1}{MO}$+$\frac{1}{NO}$=$\frac{1}{{y}_{1}+\frac{1}{2}}$+$\frac{1}{{y}_{2}+\frac{1}{2}}$=$\frac{k（{x}_{1}+{x}_{2}）+1}{{k}^{2}{x}_{1}{x}_{2}+\frac{1}{2}k（{x}_{1}+{x}_{2}）+\frac{1}{4}}$①，
联立直线y=kx和抛物线C₁解析式可得x²-kx-$\frac{1}{4}$=0，
∵x₁、x₂是方程x²-kx-$\frac{1}{4}$=0的解，
∴x₁+x₂=k，x₁x₂=-$\frac{1}{4}$，
代入①式可得：$\frac{1}{MO}$+$\frac{1}{NO}$=4，
即$\frac{1}{MO}$+$\frac{1}{NO}$为定值．

点评 本题为二次函数的综合应用，涉及函数图象与坐标轴的交点、待定系数法、圆周角定理、根与系数的关系、方程思想及分类讨论思想等知识点．在（1）中求得点B的坐标是解题的关键，在（2）中求得直线AP的解析式是解题的关键，在（3）中用k和根与系数的表示出$\frac{1}{MO}$+$\frac{1}{NO}$是解题的关键．本题考查知识点较多，综合性较强，计算量较大，难度较大．