
【题目】已知A,B两点在直线m上,C,D两点在直线n上,∠BAD=α,∠BCD=β.
(1)如图1,若∠BAD=∠ADC,求证∠ABC=∠BCD.
(2)如图2,m∥n,过点D作DE⊥BC于点E,∠BAD与∠DEB的角平分线相交于点P,求∠P(用α,β的式子表示)
(3)在(2)的条件下,若点A沿直线m向右运动,且不与B点重合,则∠APE= (用α,β的式子表示,不写证明过程).


【答案】(1)见解析;(2)∠P=![]() α+β-45°;(3)
α+β-45°;(3)![]() α+β-45°或135°+β-
α+β-45°或135°+β-![]() α
α
【解析】
(1)利用平行线的判定和性质即可证明;
(2)根据条件求出∠DEP=45°,∠BAP=∠PAD=![]() α,设AP,BC交于N,推出∠ANC=∠BAP+∠ABC=∠P+∠BEP,从而得到∠P的度数;
α,设AP,BC交于N,推出∠ANC=∠BAP+∠ABC=∠P+∠BEP,从而得到∠P的度数;
(3)分点A在点B左侧,点A在点B右侧两种情况,参照(2)中过程,分别求出∠APE的度数即可.
解:(1)∵∠BAD=∠ADC,
∴m∥n,
∴∠ABC=∠BCD;
(2)∵DE⊥BC,
∴∠DEC=∠DEB=90°,
∵∠BAD与∠DEB的角平分线相交于点P,
∴∠DEP=∠BEP=![]() ∠DEB=45°,
∠DEB=45°,
∠BAP=∠PAD=![]() ∠BAD=
∠BAD=![]() α,
α,
∵m∥n,
∴∠ABC=∠BCD=β,
设AP,BC交于N,
∵∠ANC=∠BAP+∠ABC=∠P+∠BEP,
∴![]() α+β=∠P+45°,
α+β=∠P+45°,
∴∠P=![]() α+β-45°;
α+β-45°;

(3)若点A在点B左侧,由(2)得:
∠APE=![]() α+β-45°;
α+β-45°;
若点A在点B右侧,延长EP,交AD于Q,
∴∠APE=∠PAQ+∠AQP,
∵AP平分∠BAD,
∴∠PAQ=![]() α,
α,
由(2)得∠BEP=∠DEP=45°,
∴∠AQP=∠DEP+∠ADE=45°+∠ADE,
而∠EDC=90°-∠BCD=90°-β,
∴∠ADE=180°-(90°-β)-α=90°+β-α,
∴∠AQP=45°+90°+β-α,
∴∠APE=∠PAQ+∠AQP=![]() α+45°+90°+β-α=135°+β-
α+45°+90°+β-α=135°+β-![]() α.
α.



科目:初中数学 来源: 题型:
【题目】如图,反比例函数y= ![]() 的图象经过A、B两点,过点A作AC⊥x轴,垂足为C,过点B作BD⊥x轴,垂足为D,连接AO,连接BO交AC于点E,若OC=CD,四边形BDCE的面积为1,则k的值为 .
的图象经过A、B两点,过点A作AC⊥x轴,垂足为C,过点B作BD⊥x轴,垂足为D,连接AO,连接BO交AC于点E,若OC=CD,四边形BDCE的面积为1,则k的值为 . 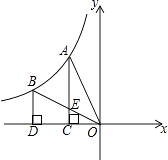
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名同学某学期的四次数学测试成绩(单位:分)如下表:
第一次 | 第二次 | 第三次 | 第四次 | |
甲 | 87 | 95 | 85 | 93 |
乙 | 80 | 80 | 90 | 90 |
据上表计算,甲、乙两名同学四次数学测试成绩的方差分别为S甲2=17、S乙2=25,下列说法正确的是( )
A.甲同学四次数学测试成绩的平均数是89分
B.甲同学四次数学测试成绩的中位数是90分
C.乙同学四次数学测试成绩的众数是80分
D.乙同学四次数学测试成绩较稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,AC∥BE,∠MAC=40,∠D=50°,CH平分∠ACD,BH平分∠ABD,
(1)求∠EBH的角度
(2)求∠BHC的角度

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直角∠EPF的顶点和正方形ABCD的顶点C重合,两直角边PE,PF分别和AB,AD所在的直线交于点E和F.易得△PBE≌△PDF,故结论“PE=PF”成立; 
(1)如图2,若点P在正方形ABCD的对角线AC上,其他条件不变,(1)中的结论是否仍然成立?说明理由; 
(2)如图(3)将(2)中正方形ABCD改为矩形ABCD其他条件不变,若AB=m,BC=n,直接写出 ![]() 的值.
的值. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,∠A=90°,BC=4,点P是△ABC边上一动点,沿B→A→C的路径移动,过点P作PD⊥BC于点D,设BD=x,△BDP的面积为y,则下列能大致反映y与x函数关系的图象是( )
A.
B.
C.
D.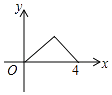
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校新到一批理、化、生实验器材需要整理,若实验管理员李老师一人单独整理需要40分钟完成,现在李老师与工人王师傅共同整理20分钟后,李老师因事外出,王师傅再单独整理了20分钟才完成任务.
(1)王师傅单独整理这批实验器材需要多少分钟?
(2)学校要求王师傅的工作时间不能超过30分钟,要完成整理这批器材,李老师至少要工作多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
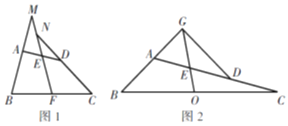
【题目】(1)如图1,在四边形ABCD中,F、E分别是BC、AD的中点,连结EF并延长,分别与BA、CD的延长线交于点M、N,则∠BME=∠CNE,求证:AB=CD;(提示取BD的中点H,连结FH,HE作辅助线)
(2)如图2,在△ABC中,且O是BC边的中点,D是AC边上一点,E是AD的中点,直线OE交BA的延长线于点G,若AB=DC=5,∠OEC=60°,求OE的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com