练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．若规定[a]表示不超过a的最大整数，例如[4.3]=4，若m=[π+1]，n=[-2.1]，则在此规定下[m+$\frac{7}{4}$n]的值为（　　）
    A．-3B．-2C．-1D．0

    分析 先计算出m+$\frac{7}{4}$n，再根据[a]的规定解答．

    解答 解：∵m=[π+1]，n=[-2.1]，
    ∴m+$\frac{7}{4}$n=π+1+$\frac{7}{4}$×（-2.1）=π+1-3.675=π-2.675，
    ∴[m+$\frac{7}{4}$n]=0．
    故选D．

    点评 本题考查了有理数的大小比较，新定义，读懂题目信息并理解规定是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    16．如图，已知P是线段AB上一点，AP=$\frac{2}{3}$AB，C，D两点从A，P同时出发，分别以每秒2厘米，每秒1匣米的速度沿AB方向运动，当点D到达终点B时，点C也停止运动，设AB=a（厘米），点C，D的运动时间为t（秒）．
    （1）用含a和t的代数式表示线段CP的长度；
    （2）当t=5时，CD=$\frac{1}{2}$AB，求线段AB的长；
    （3）当CB-AC=PC时，求$\frac{PD}{AB}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．计算：
    （1）24+（-22）-（+10）+（-13）
    （2）（-1.5）+4$\frac{1}{4}$+2.75+（-5$\frac{1}{2}$）
    （3）（-81）÷$\frac{9}{4}$×$\frac{4}{9}$÷（-16）
    （4）-14-$\frac{1}{7}$×[2-（-4）2]．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．按程序运算（如图所示）：

    例如，输入x=5时，则运算的结果为299，若使运算结果为363，那么所有满足条件x（x为正整数）的值是6、23、91．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

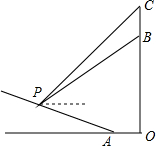    16．如图，某高楼OB上有一旗杆CB，我校数学兴趣小组的同学准备利用所学的三角函数知识估测该高楼的高度，由于有其他建筑物遮挡视线不便测量，所以测量员沿坡度i=1：$\sqrt{3}$的山坡从坡脚的A处前行50米到达P处，测得旗杆顶部C的仰角为45°，旗杆底部B的仰角为37°（测量员的身高忽略不计），已知旗杆高BC=15米，则该高楼OB的高度为（　　）米．（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）
    A．45B．60C．70D．85

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．若一个三角形的两边长分别为2，7，且第三边的长为奇数，则这个三角形的周长为16．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．在△ABC中，∠C=90°，AC=BC，则△ABC的一个锐角的余弦值等于$\frac{\sqrt{2}}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．某宾馆有40个房间供游客居住，当每个房间每天的定价为160元时，房间会全部住满；当每个房间每天的定价每增加10元时，就会有一个房间空闲．如果游客居住房间，宾馆需对每个房间每天支出20元的各种费用．设每间每天房价定为x元，宾馆每天利润为y元，则y与x的函数关系式为y=-$\frac{{x}^{2}}{10}$+58x-1120．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．如图，在△ABC，E是BC上一点，EC=2BE，点D是AC的中点，且S△ABC=24，则S△ADF-S△BEF=4．

    查看答案和解析>>

    同步练习册答案