
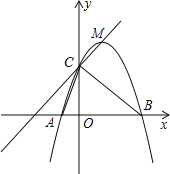
【题目】如图,二次函数![]() 的图象与x轴交于
的图象与x轴交于![]() 两点,其中点
两点,其中点![]() ,点
,点![]() ,点
,点![]() 都在抛物线上,M为抛物线的顶点.
都在抛物线上,M为抛物线的顶点.
![]() 求抛物线的函数解析式;
求抛物线的函数解析式;
![]() 求
求![]() 的面积;
的面积;
![]() 根据图形直接写出使一次函数值大于二次函数值的x的取值范围.
根据图形直接写出使一次函数值大于二次函数值的x的取值范围.
【答案】(1)![]() ;(2)15;(3)
;(2)15;(3)![]() 或
或![]() .
.
【解析】试题分析:
(1)将所A、C、D的坐标代入![]() 列出方程组,解方程组求得a、b、c的值,即可得到抛物线的解析式;
列出方程组,解方程组求得a、b、c的值,即可得到抛物线的解析式;
(2)先根据(1)中所得解析式求出点B和点M的坐标,连接OM,即可由S△MCB=S△MOC+S△MOB-S△BOC求得△MCB的面积;
(3)由图形结合点M和点C的坐标写出一次函数图象在二次函数图象上方时所对应的x的取值范围即可.
试题解析:
(1)∵二次函数![]() 的图象经过点
的图象经过点![]() ,点
,点![]() ,点
,点![]() ,
,
∴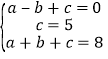 ,解得:
,解得: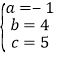 ,
,
∴该二次函数的解析式为:![]() ;
;
(2)在![]() 中,当
中,当![]() 时,有
时,有![]() ,解得:
,解得:![]() ,
,
∴点B的坐标为(5,0),
∵![]() ,
,
∴二次函数图象的顶点M的坐标为:(2,9),
如图,连接OM,BM,则:
S△BMC=S△OMC+S△OMB-S△BOC
=![]()
=15.
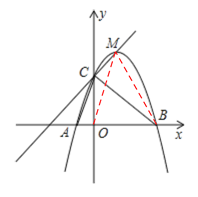
(3)由图可知在点C的左侧和点M的右侧时,一次函数的图象在二次函数图象的上方,
∴当一次函数的值大于二次函数的值时,所对应的![]() 的取值范围是:
的取值范围是:![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
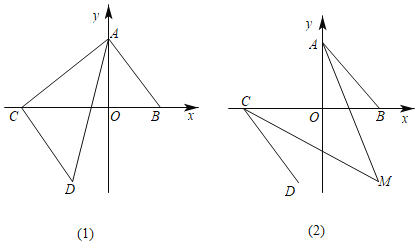
【题目】如图,在平面直角坐标系中,已知点A(0,4),B(3,0),线段AB平移后对应的线段为CD,点C在x轴的负半轴上,B、C两点之间的距离为8.
(1)求点D的坐标;
(2)如图(1),求△ACD的面积;
(3)如图(2),∠OAB与∠OCD的角平分线相交于点M,探求∠AMC的度数并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系xOy中,直线AB与x轴、y轴的交点分别为A、![]() ,将
,将![]() 对折,使点O的对应点H恰好落在直线AB上,折痕交x轴于点C,
对折,使点O的对应点H恰好落在直线AB上,折痕交x轴于点C,
![]() 求过A、B、C三点的抛物线解析式;
求过A、B、C三点的抛物线解析式;
![]() 若抛物线的顶点为D,在直线BC上是否存在点P,使得四边形ODAP为平行四边形?若存在,求出点P的坐标;若不存在,说明理由;
若抛物线的顶点为D,在直线BC上是否存在点P,使得四边形ODAP为平行四边形?若存在,求出点P的坐标;若不存在,说明理由;
![]() 若点Q是抛物线上一个动点,使得以A、B、Q为顶点并且以AB为直角边的直角三角形,直接写出Q点坐标.
若点Q是抛物线上一个动点,使得以A、B、Q为顶点并且以AB为直角边的直角三角形,直接写出Q点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的平面直角坐标系中,一只蚂蚁从A点出发,沿着A-B-C-D-A…循环爬行,其中A点坐标为(1,-1),B点坐标为(-1,-1),C点坐标为(-1,3),D点坐标为(1,3),当蚂蚁爬了2 018个单位长度时,它所处位置的坐标为_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与
与![]() 轴只有一个公共点.
轴只有一个公共点.
(![]() )求
)求![]() 的值.
的值.
(![]() )怎样平移抛物线
)怎样平移抛物线![]() 就可以得到抛物线
就可以得到抛物线![]() ?请写出具体的平移方法.
?请写出具体的平移方法.
(![]() )若点
)若点![]() 和点
和点![]() 都在抛物线
都在抛物线![]() 上,且
上,且![]() ,直接写出
,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店用6000元购进A,B两种新式服装,按标价售出后可获得毛利润3800元(毛利润=售价-进价).这两种服装的进价,标价如表所示.

(1)求这两种服装各购进的件数;
(2)如果A种服装按标价的8折出售,B种服装按标价的7折出售,那么这批服装全部售完后,服装店比按标价出售少收入多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com