
如图,点E是DF上一点,点B在AC上,∠1=∠2,∠C=∠D,试说明DF∥AC的理由。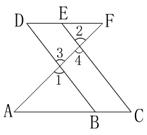
理由:∵∠1=∠2 (已知)
∠1=∠3,∠2=∠4 ( )
∴∠3=∠4 ( )
∴______∥______ ( )
∴∠C=∠DBA ( )
又∵∠C=∠D ( 已知 )
∴∠DBA=∠D ( )
∴DF∥AC ( )
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
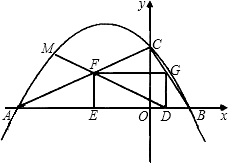 抛物线对称轴为直线x=-3.
抛物线对称轴为直线x=-3.| 2 | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 22、将两个等边△ABC和△DEF(DE>AB)如图所示摆放,点D是BC上的一点(除B、C点外).把△DEF绕顶点D顺时针旋转一定的角度,使得边DE、DF与△ABC的边(除BC边外)分别相交于点M、N.
22、将两个等边△ABC和△DEF(DE>AB)如图所示摆放,点D是BC上的一点(除B、C点外).把△DEF绕顶点D顺时针旋转一定的角度,使得边DE、DF与△ABC的边(除BC边外)分别相交于点M、N.查看答案和解析>>
科目:初中数学 来源: 题型:
如图①,点C将线段AB分成两部分,如果 ,那么称点C为线段AB的黄金分割点.某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1、S2,如果
,那么称点C为线段AB的黄金分割点.某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1、S2,如果![]() ,那么称直线l为该图形的黄金分割线.
,那么称直线l为该图形的黄金分割线.
1.研究小组猜想:在△ABC中,若点D为AB边上的黄金分割点,如图②所示,则直线CD是△ABC的黄金分割线.你认为对吗?为什么?
2.请你说明:三角形的中线是否也是该三角形的黄金分割线?
3.研究小组在进一步探究中发现:过点C任意作一条直线交AB于点E,再过点D作直线DF∥CE,交AC于点F,连接EF,如图③所示,则直线EF也是△ABC的黄金分割线.请你说明理由.
4.如图④,点E是□ABCD的边AB上的黄金分割点,过点E作EF∥AD,交DC于点F,显然直线EF是□ABCD的黄金分割线,请你画一条□ABCD的黄金分割线,使它不经过□ABCD各边黄金分割点.

查看答案和解析>>
科目:初中数学 来源:2011~2012学年江苏苏州八年级下期期末复习(一)数学试卷(带解析) 题型:解答题
如图①,点C将线段AB分成两部分,如果 ,那么称点C为线段AB的黄金分割点.某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1、S2,如果
,那么称点C为线段AB的黄金分割点.某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1、S2,如果 ,那么称直线l为该图形的黄金分割线.
,那么称直线l为该图形的黄金分割线.
【小题1】研究小组猜想:在△ABC中,若点D为AB边上的黄金分割点,如图②所示,则直线CD是△ABC的黄金分割线.你认为对吗?为什么?
【小题2】请你说明:三角形的中线是否也是该三角形的黄金分割线?
【小题3】研究小组在进一步探究中发现:过点C任意作一条直线交AB于点E,再过点D作直线DF∥CE,交AC于点F,连接EF,如图③所示,则直线EF也是△ABC的黄金分割线.请你说明理由.
【小题4】如图④,点E是□ABCD的边AB上的黄金分割点,过点E作EF∥AD,交DC于点F,显然直线EF是□ABCD的黄金分割线,请你画一条□ABCD的黄金分割线,使它不经过□ABCD各边黄金分割点.
查看答案和解析>>
科目:初中数学 来源:2013届江苏苏州八年级下期期末复习(一)数学试卷(解析版) 题型:解答题
如图①,点C将线段AB分成两部分,如果 ,那么称点C为线段AB的黄金分割点.某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1、S2,如果
,那么称点C为线段AB的黄金分割点.某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1、S2,如果 ,那么称直线l为该图形的黄金分割线.
,那么称直线l为该图形的黄金分割线.
1.研究小组猜想:在△ABC中,若点D为AB边上的黄金分割点,如图②所示,则直线CD是△ABC的黄金分割线.你认为对吗?为什么?
2.请你说明:三角形的中线是否也是该三角形的黄金分割线?
3.研究小组在进一步探究中发现:过点C任意作一条直线交AB于点E,再过点D作直线DF∥CE,交AC于点F,连接EF,如图③所示,则直线EF也是△ABC的黄金分割线.请你说明理由.
4.如图④,点E是□ABCD的边AB上的黄金分割点,过点E作EF∥AD,交DC于点F,显然直线EF是□ABCD的黄金分割线,请你画一条□ABCD的黄金分割线,使它不经过□ABCD各边黄金分割点.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com