
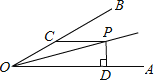
【题目】如图,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4,则PD的长为 .
【答案】2
【解析】
试题分析:过P作PE垂直与OB,由∠AOP=∠BOP,PD垂直于OA,利用角平分线定理得到PE=PD,由PC与OA平行,根据两直线平行得到一对内错角相等,又OP为角平分线得到一对角相等,等量代换可得∠COP=∠CPO,又∠ECP为三角形COP的外角,利用三角形外角的性质求出∠ECP=30°,在直角三角形ECP中,由30°角所对的直角边等于斜边的一半,由斜边PC的长求出PE的长,即为PD的长.
解:过P作PE⊥OB,交OB与点E,

∵∠AOP=∠BOP,PD⊥OA,PE⊥OB,
∴PD=PE,
∵PC∥OA,
∴∠CPO=∠POD,
又∠AOP=∠BOP=15°,
∴∠CPO=∠BOP=15°,
又∠ECP为△OCP的外角,
∴∠ECP=∠COP+∠CPO=30°,
在直角三角形CEP中,∠ECP=30°,PC=4,
∴PE=![]() PC=2,
PC=2,
则PD=PE=2.
故答案为:2.


科目:初中数学 来源: 题型:
【题目】要得到y=﹣2(x+2)2﹣3的图象,需将抛物线y=﹣2x2作如下平移( )
A. 向右平移2个单位,再向上平移3个单位
B. 向右平移2个单位,再向下平移3个单位
C. 向左平移2个单位,再向上平移3个单位
D. 向左平移2个单位,再向下平移3个单位
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一元二次方程 x2﹣3x+5=0的根的情况是( )
A. 有两个不相等的实数根 B. 有两个相等的实数根
C. 只有一个实数根 D. 没有实数根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列结论错误的是( )
A.全等三角形对应边上的中线相等
B.两个直角三角形中,两个锐角相等,则这两个三角形全等
C.全等三角形对应边上的高相等
D.两个直角三角形中,斜边和一个锐角对应相等,则这两个三角形全等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,直线y=x+3交x轴于A点,交y轴于B点,过A、B两点的抛物线y=-x2+bx+c交x轴于另一点C,点D是抛物线的顶点.
中,直线y=x+3交x轴于A点,交y轴于B点,过A、B两点的抛物线y=-x2+bx+c交x轴于另一点C,点D是抛物线的顶点.
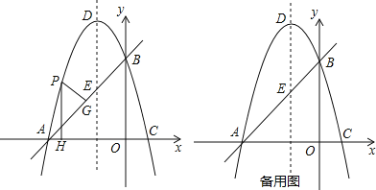
(1)求此抛物线的解析式;
(2)点P是直线AB上方的抛物线上一点(不与点A、B重合),过点P作x轴的垂线交x轴于点H,交直线AB于点F,作PG⊥AB于点G.求出△PFG的周长最大值;
(3)在抛物线![]() 上是否存在除点D以外的点M,使得△ABM与△ABD的面积相等?若存在,请求出此时点M的坐标;若不存在,请说明理由.
上是否存在除点D以外的点M,使得△ABM与△ABD的面积相等?若存在,请求出此时点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC、AC分别交于D、E两点,DF⊥AC于F.
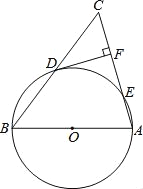
(1)求证:DF为⊙O的切线;
(2)若cosC=![]() ,CF=9,求AE的长.
,CF=9,求AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com