Question

13．已知抛物线y=ax²+2（a+1）x+$\frac{3}{2}$（a≠0）与x轴交于A（x₁，0）、B（x₂，0）（x₁＜x₂）两点，与y轴交于C点．经过第三象限中的定点D．
（1）直接写出C、D两点的坐标．
（2）当x=x₀时，二次函数的值记住为y₀，若存在点（x₀，y₀），使y₀=x₀成立，则称点（x₀，y₀）为抛物线上的不动点，求证：抛物线y=ax²+2（a+1）x+$\frac{3}{2}$存在两个不动点．
（3）当△ABD的面积等于△CBD时，求a的值．

Answer 1

分析 （1）令x=0即可求出C点坐标，由定点可知在解析式中含有字母a的单项式之和为0，即可求出对应的x的值；进而求出点D坐标；
（2）令x=y=x₀，运用一元二次方程的根的判别式即可进行证明；
（3）表示三角形面积根据题意列方程求解即可．

解答 解：（1）y=ax²+2（a+1）x+$\frac{3}{2}$，令x=0，解得y=$\frac{3}{2}$，
∴C（0，$\frac{3}{2}$），
y=ax²+2（a+1）x+$\frac{3}{2}$=$a{x}^{2}+2ax+2x+\frac{3}{2}$，
由题意可得：ax²+2ax=0，
解得：x=-2，或x=0（舍去）
当x=-2时，y=-$\frac{5}{2}$，
∴D（-2，-$\frac{5}{2}$）；
（2）由题意可得：
x₀=$a{{x}_{0}}^{2}+2（a+1）{x}_{0}+\frac{3}{2}$，
$a{{x}_{0}}^{2}+（2a+1）{x}_{0}+\frac{3}{2}=0$，
△=$（2a+1）^{2}-4×\frac{3}{2}a$=4$（a-\frac{1}{4}）^{2}+\frac{3}{4}$＞0，
所以方程总有两个不相等的实数根，抛物线y=ax²+2（a+1）x+$\frac{3}{2}$存在两个不动点；
（3）如图1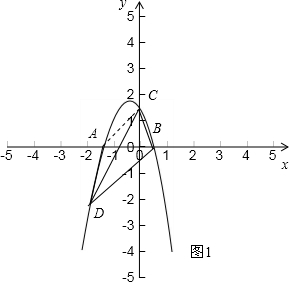

连接AC，由△ABD的面积等于△CBD可知AC∥BD，
y=ax²+2（a+1）x+$\frac{3}{2}$（a≠0），令y=0，得
x=$\frac{-2a-2-\sqrt{4{a}^{2}+2a+4}}{2a}$或x=$\frac{-2a-2+\sqrt{4{a}^{2}+2a+4}}{2a}$，
可知A（$\frac{-2a-2-\sqrt{4{a}^{2}+2a+4}}{2a}$，0），B（$\frac{-2a-2+\sqrt{4{a}^{2}+2a+4}}{2a}$，0），
又OC=$\frac{3}{2}$，D（-2，-$\frac{5}{2}$），
由AC∥BD可得，
$\frac{\frac{3}{2}}{\frac{-2a-2-\sqrt{4{a}^{2}+2a+4}}{-2a}}$=$\frac{\frac{5}{2}}{\frac{-2a-2+\sqrt{4{a}^{2}+2a+4}}{2a}+2}$，
解得：a=-2．

点评 此题主要考查二次函数综合问题，会求交点坐标，会分析定点的问题，知道运用平行建立适当的关系列方程并准确求解是解题的关键．