
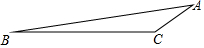
 如图,在△ABC中,∠C=150°,AC=2,tanB=$\frac{1}{8}$.
如图,在△ABC中,∠C=150°,AC=2,tanB=$\frac{1}{8}$.分析 (1)作辅助线AD⊥BC,交BC的延长线于点D,然后根据在△ABC中,∠C=150°,AC=2,tanB=$\frac{1}{8}$,可以求得∠ACD的度数,从而可以得到AD、CD、BD的长,进而求得BC的长;
(2)作辅助线CE=AC,可以得到∠AEC=15°,然后求出tan∠AEC的值即可解答本题.
解答 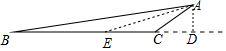 解:(1)作AD⊥BC,交BC的延长线于点D,如右图所示,
解:(1)作AD⊥BC,交BC的延长线于点D,如右图所示,
∵在△ABC中,∠C=150°,AC=2,tanB=$\frac{1}{8}$,AD⊥BC,
∴∠ACD=30°,∠ADC=90°,
∴AD=$\frac{1}{2}AC$=1,
∴CD=$\sqrt{A{C}^{2}-A{D}^{2}}=\sqrt{{2}^{2}-{1}^{2}}=\sqrt{3}$,
∴BD=$\frac{AD}{tanB}=\frac{1}{\frac{1}{8}}=8$,
∴BC=BD-CD=8-$\sqrt{3}$;
(2)在BC上截取线段CE=AC,如右上图所示,
∵∠C=150°,
∴∠AEC=∠EAC=15°,
∵AD⊥BC,AC=2,CE=AC,AD=1,CD=$\sqrt{3}$,
∴∠ADE=90°,EC=2,
∴ED=EC+CD=2+$\sqrt{3}$,
∴tan∠AED=$\frac{AD}{ED}=\frac{1}{2+\sqrt{3}}=2-\sqrt{3}$,
即 tan15°=2-$\sqrt{3}$.
点评 本题考查解直角三角形,解答此类问题的关键是作出合适的辅助线,然后根据锐角三角函数和勾股定理解答.


科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{8}$÷$\sqrt{2}$=2 | B. | 5$\sqrt{3}$•5$\sqrt{2}$=5$\sqrt{6}$ | C. | 2$\sqrt{3}$+3$\sqrt{2}$=5$\sqrt{6}$ | D. | $\sqrt{(-6)^{2}}$=-6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1207×108元 | B. | 12.07×1010元 | C. | 1.207×108元 | D. | 1.207×1011元 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{a-b}{2}$ | B. | $\frac{x-3}{x}$ | C. | $\frac{5+y}{π}$ | D. | -$\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{7}{25}$ | B. | $\frac{7}{32}$ | C. | $\frac{3}{80}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com