
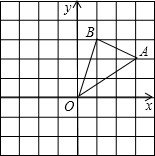
 如图,在边长为1的正方形组成的网格中建立直角坐标系,△AOB的顶点均在格点上,点O为原点,点A,B的坐标分别是(3,2)、B(1,3).
如图,在边长为1的正方形组成的网格中建立直角坐标系,△AOB的顶点均在格点上,点O为原点,点A,B的坐标分别是(3,2)、B(1,3).分析 (1)利用网格特点和点平移的规律得到点A1、B1、O1,的坐标,然后描点得到△A1B1O1;
(2)利用网格特点和旋转的性质画出点A、B对应点A2、B2,则可得到△A2B2O,再写出点A2的坐标;
(3)线段OA扫过的图形是以O为圆心,OA为半径,圆心角为90度的扇形,则利用扇形面积公式可计算出线段OA扫过的图形的面积.
解答 解:(1)如图,△A1O1B1为所作,点B1的坐标为(1,0);
(2)如图,△A2OB2为所作,点A2的坐标为(-2,3);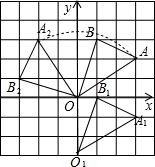
(3)OA=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$,
所以在(2)中的旋转过程中,线段OA扫过的图形的面积=$\frac{90•π•(\sqrt{13})^{2}}{360}$=$\frac{\sqrt{13}}{4}$π.
故答案为(1,0),(-2,3),$\frac{\sqrt{13}}{4}$π.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了平移变换.


科目:初中数学 来源: 题型:解答题
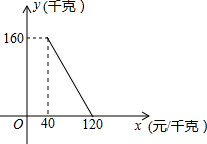 某商店以40元/千克的单价新进一批茶叶,经调查发现,在一段时间内,销售量y(千克)与销售x(元/千克)之间函数关系如图所示.
某商店以40元/千克的单价新进一批茶叶,经调查发现,在一段时间内,销售量y(千克)与销售x(元/千克)之间函数关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在等腰△ABC中,AB=BC=4,把△ABC沿AC翻折得到△ADC.则
如图,在等腰△ABC中,AB=BC=4,把△ABC沿AC翻折得到△ADC.则查看答案和解析>>
科目:初中数学 来源: 题型:填空题
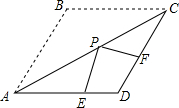
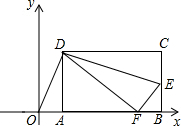 如图,矩形ABCD的顶点AB在x轴上,点D的坐标为(3,4),点E在边BC上,△CDE沿DE翻折后点C恰好落在x轴上点F处,若△ODF为等腰三角形,点C的坐标为(8,4)或(3$+2\sqrt{5}$,4)或($\frac{43}{6}$,4).
如图,矩形ABCD的顶点AB在x轴上,点D的坐标为(3,4),点E在边BC上,△CDE沿DE翻折后点C恰好落在x轴上点F处,若△ODF为等腰三角形,点C的坐标为(8,4)或(3$+2\sqrt{5}$,4)或($\frac{43}{6}$,4).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
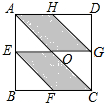 如图,正方形ABCD是一块绿化带,E,F,G,H分别是AB,BC,CD,AD的中点,阴影部分EOCF,AOGH都是花圃,一只自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟在花圃上的概率为( )
如图,正方形ABCD是一块绿化带,E,F,G,H分别是AB,BC,CD,AD的中点,阴影部分EOCF,AOGH都是花圃,一只自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟在花圃上的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
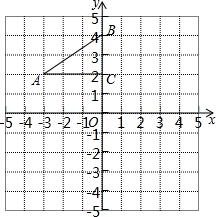 如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).
如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com