
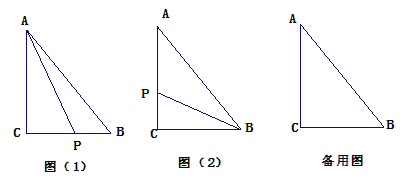
【题目】如图(1)在△ABC中,∠C=90°,AB=25cm,BC=15cm,若动点P从点C开始沿着C→B→A→C的路径运动,且速度为每秒5cm,设点P运动的时间为t秒.
(1)点P运动2秒后,求△ABP的面积;
(2)如图(2),当t为何值时,BP平分∠ABC;
(3)当△BCP为等腰三角形时,直接写出所有满足条件t的值.
【答案】(1)50(2)10.5(3)5.5、6、6.6、9
【解析】
(1)根据勾股定理求得AC=20,根据运动的速度和时间求得CP=10,BP=5,即可得到△ABP的面积;
(2)过点P作PD⊥AB于点D,判定Rt△BPD≌Rt△BPC(HL),得到BD=BC=15,AD=10,再设PC=x,则PD=x,AP=20﹣x.在Rt△APD中,根据勾股定理得到PD2+AD2=AP2,即x2+102=(20﹣x)2,解方程即可得到结论;
(3)分三种情况讨论:①作CB的垂直平分线交AB于P,连接CP,则CP=BP;②以B为圆心,CB为半径作弧交AB于点P,则CB=PB=15;③以C为圆心,CB为半径作弧交AB于P1,交AC于点P2,过C作CD⊥AB于D,则CP1=CB,CP2=CB=15,分别求解即可.
(1)如图1.
∵∠C=90°,AB=25,BC=15,∴AC=![]() =20.
=20.
∵CP=5×2=10,BP=BC-PC=15-10=5,∴△ABP的面积=![]() ×PB×AC=
×PB×AC=![]() ×5×20=50(cm2).
×5×20=50(cm2).
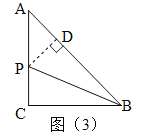
(2)如图(3),过点P作PD⊥AB于点D.
∵BP平分∠ABC,∴PD=PC.在Rt△BPD和Rt△BPC中,∵![]() ,∴Rt△BPD≌Rt△BPC(HL),∴BD=BC=15,∴AD=25﹣15=10,设PC=x,则PD=x,AP=20﹣x.在Rt△APD中,PD2+AD2=AP2,即x2+102=(20﹣x)2,解得:x=7.5,∴t=(CB+BA+AC-PC)÷5=(15+25+20-7.5)÷5=10.5.
,∴Rt△BPD≌Rt△BPC(HL),∴BD=BC=15,∴AD=25﹣15=10,设PC=x,则PD=x,AP=20﹣x.在Rt△APD中,PD2+AD2=AP2,即x2+102=(20﹣x)2,解得:x=7.5,∴t=(CB+BA+AC-PC)÷5=(15+25+20-7.5)÷5=10.5.
故t=10.5秒时,BP平分∠ABC.
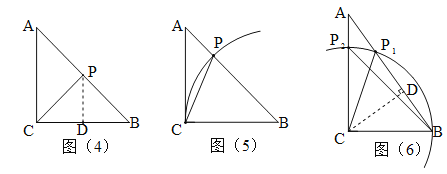
(3)分三种情况讨论:①如图(4),作CB的垂直平分线交AB于P,连接CP,则CP=BP.
∵AC⊥BC,PD⊥BC,∴AC∥PD.
∵CD=DB,∴AP=PB=![]() AB=12.5,∴t=(CB+BP)÷5=(15+12.5)÷5=5.5;
AB=12.5,∴t=(CB+BP)÷5=(15+12.5)÷5=5.5;
②如图(5),以B为圆心,CB为半径作弧交AB于点P,则CB=PB=15,∴t=(CB+BP)÷5=(15+15)÷5=6;
③如图(6),以C为圆心,CB为半径作弧交AB于P1,交AC于点P2,过C作CD⊥AB于D,则CP1=CB,CP2=CB,CD=![]() =
=![]() =12.
=12.
∵CP1=CB,CD⊥AB,∴BD=DP1=![]() =9,∴BP1=2BD=18,∴t=(15+18)÷5=6.6;
=9,∴BP1=2BD=18,∴t=(15+18)÷5=6.6;
∵CP2=CB=15,∴t=(CB+BA+AC-CP2)÷5=(15+25+20-15)÷5=9.
综上所述:当△BCP为等腰三角形时,t的值为:5.5,6,6.6,9.


科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+b2﹣4ac与反比例函数y= ![]() 在同一坐标系内的图象大致为( )
在同一坐标系内的图象大致为( ) 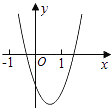
A.
B.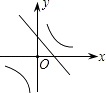
C.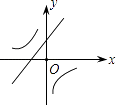
D.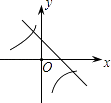
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个横断面为抛物线形状的拱桥,当水面宽4m时,拱顶(拱桥洞的最高点)离水面2m,当水面下降1m时,水面的宽度为( )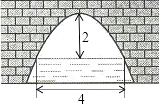
A.3
B.2 ![]()
C.3 ![]()
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=900,∠B=∠E=300.
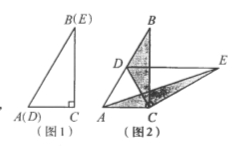


(1)操作发现如图2,固定△ABC,使△DEC绕点C旋转。当点D恰好落在BC边上时,填空:线段DE与AC的位置关系是 ;
② 设△BDC的面积为S1,△AEC的面积为S2。则S1与S2的数量关系是 。
(2)猜想论证
当△DEC绕点C旋转到图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC,CE边上的高,请你证明小明的猜想。
(3)拓展探究
已知∠ABC=600,点D是其角平分线上一点,BD=CD=4,OE∥AB交BC于点E(如图4),若在射线BA上存在点F,使S△DCF =S△BDC,请直接写出相应的BF的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△OAB的顶点A(﹣2,4)在抛物线y=ax2上,将Rt△OAB绕点O顺时针旋转90°,得到△OCD,边CD与该抛物线交于点P,则点P的坐标为( )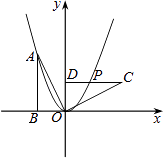
A.( ![]() ,
, ![]() )
)
B.(2,2)
C.( ![]() ,2)
,2)
D.(2, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某青春党支部在精准扶贫活动中,给结对帮扶的贫困家庭赠送甲、乙两种树苗让其栽种.已知乙种树苗的价格比甲种树苗贵10元,用480元购买乙种树苗的棵数恰好与用360元购买甲种树苗的棵数相同.
(1)求甲、乙两种树苗每棵的价格各是多少元?
(2)在实际帮扶中,他们决定再次购买甲、乙两种树苗共50棵,此时,甲种树苗的售价比第一次购买时降低了10%,乙种树苗的售价不变,如果再次购买两种树苗的总费用不超过1500元,那么他们最多可购买多少棵乙种树苗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,△ABC顶点的横、纵坐标都是整数.若将△ABC以某点为旋转中心,顺时针旋转90°得到△DEF,则旋转中心的坐标是( )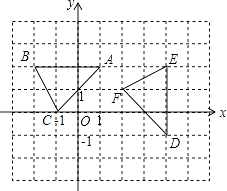
A.(0,0)
B.(1,0)
C.(1,﹣1)
D.(2.5,0.5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线相交于坐标原点,点A的坐标为(a,2),点B的坐标为(﹣1,﹣ ![]() ),点C的坐标为(2
),点C的坐标为(2 ![]() ,c),那么a,c的值分别是( )
,c),那么a,c的值分别是( ) 
A.a=﹣1,c=﹣ ![]()
B.a=﹣2 ![]() ,c=﹣2
,c=﹣2
C.a=1,c= ![]()
D.a=2 ![]() ,c=2
,c=2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC内接于⊙O,点D在OC的延长线上,sinB= ![]() ,∠CAD=30°.
,∠CAD=30°.
(1)求证:AD是⊙O的切线;
(2)若OD⊥AB,BC=5,求AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com