
 如图,在正△ABC中,D、E分别在AC、AB上,且$\frac{AD}{AC}=\frac{1}{3}$,AE=BE,则有( )
如图,在正△ABC中,D、E分别在AC、AB上,且$\frac{AD}{AC}=\frac{1}{3}$,AE=BE,则有( )| A. | △AED∽△ABC | B. | △ADB∽△BED | C. | △BCD∽△ABC | D. | △AED∽△CBD |
分析 根据等边三角形的性质得出角相等,再由已知条件求出$\frac{AD}{CD}=\frac{AE}{BC}$,即两边对应成比例并且夹角相等,因此两个三角形相似.
解答 解:∵△ABC是等边三角形,$\frac{AD}{AC}$=$\frac{1}{3}$,
∴AB=BC=AC,∠A=∠C,
设AD=x,AC=3x,
则BC=3x,CD=2x,
∵AE=BE=$\frac{3}{2}$x,
∴$\frac{AD}{CD}=\frac{1}{2}$,$\frac{AE}{BC}=\frac{1}{2}$,
∴$\frac{AD}{CD}=\frac{AE}{BC}$,
∴△AED∽△CBD;
故选:D.
点评 本题考查了相似三角形的判定方法、等边三角形的性质;熟练掌握相似三角形的判定方法是解决问题的关键.


科目:初中数学 来源: 题型:选择题
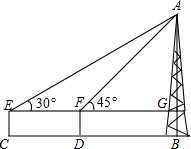 周末,小明和小华来滨湖新区渡江纪念馆游玩,看到高雄挺拔的“胜利之塔”,萌发了用所学知识测量塔高的想法,如图,他俩在塔AB前的平地上选择一点C,树立测角仪CE,测出看塔顶的仰角约为30°,从C点向塔底B走70米到达D点,测出看塔顶的仰角约为45°,已知测角仪器高为1米,则塔AB的高大约为($\sqrt{3}$≈1.7)( )
周末,小明和小华来滨湖新区渡江纪念馆游玩,看到高雄挺拔的“胜利之塔”,萌发了用所学知识测量塔高的想法,如图,他俩在塔AB前的平地上选择一点C,树立测角仪CE,测出看塔顶的仰角约为30°,从C点向塔底B走70米到达D点,测出看塔顶的仰角约为45°,已知测角仪器高为1米,则塔AB的高大约为($\sqrt{3}$≈1.7)( )| A. | 141米 | B. | 101米 | C. | 91米 | D. | 96米 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,2),且与X轴交点的横坐标分别为x1,x2,其中-2<x1<-1,0<x2<1,下列结论:
如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,2),且与X轴交点的横坐标分别为x1,x2,其中-2<x1<-1,0<x2<1,下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com