练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在△ABC中，AB=AC,点D是边AC上一点，BC=BD=AD,则∠A的大小是（　　　）．

    A. 36° B. 54° C. 72° D. 30°

    【答案】A

    【解析】

    由BD=BC=AD可知，△ABD，△BCD为等腰三角形，设∠A=∠ABD=x，则∠C=∠CDB=2x，又由AB=AC可知，△ABC为等腰三角形，则∠ABC=∠C=2x．在△ABC中，用内角和定理列方程求解．

    ∵BD=BC=AD，∴△ABD，△BCD为等腰三角形，设∠A=∠ABD=x，则∠C=∠CDB=2x．

    又∵AB=AC，∴△ABC为等腰三角形，∴∠ABC=∠C=2x．在△ABC中，∠A+∠ABC+∠C=180°，即x+2x+2x=180°，解得：x=36°，即∠A=36°．

    故选A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，AB是半圆O的直径，点P在BA的延长线上，PD切⊙O于点C，BD⊥PD，垂足为D，连接BC．
    （1）求证：BC平分∠PBD；
    （2）求证：BC2=ABBD；
    （3）若PA=6，PC=6 ，求BD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，BP是△ABC中∠ABC的平分线，CP是△ABC的外角∠ACM的平分线，如果∠ABP＝20°，∠ACP＝50°，那么∠A＋∠P的度数为(　　)

    A. 60° B. 70° C. 80° D. 90°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

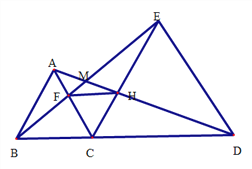
    【题目】如图，已知△ABC和△ECD都是等边三角形， B、C、D在一条直线上。

    求证：（1）BE=AD；

    （2）CF=CH；

    （3）△FCH是等边三角形；

    （4）FH∥BD；

    （5）求∠EMD的度数。；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知在△ABC中，∠B=90°，AB=8cm，BC=6cm，点P从点A开始沿△ABC的边做逆时针运动，且速度为每秒1cm；点Q从点B开始沿△ABC的边做逆时针运动，且速度为每秒2cm，他们同时出发，设运动时间为t秒．

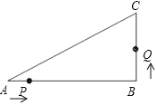
    （1）出发2秒后，P，Q两点间的距离为多少cm？

    （2）在运动过程中，△PQB能形成等腰三角形吗？若能，请求出几秒后第一次形成等腰三角形；若不能，则说明理由.

    （3）出发几秒后，线段PQ第一次把△ABC的周长分成相等两部分？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为鼓励节约能源，某电力公司特别出台了新的用电收费标准：当每户每月用电量不超过210度时，收费标准是每度0.5元；当每户每月用电量超过210度时，超出部分的收费标准是每度0.8元．

    (1)小林家在4月份用电度，请你用来表示小林家在4月份应付的电费：_________；

    (2)小林家在12月份交付电费181元，请你利用方程的知识，求小林家在12月份的用电量．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】规定：[x]表示不大于x的最大整数，（x）表示不小于x的最小整数，[x）表示最接近x的整数（x≠n+0.5，n为整数），例如：[2.3]=2，（2.3）=3，[2.3）=2．则下列说法正确的是 ． （写出所有正确说法的序号） ①当x=1.7时，[x]+（x）+[x）=6；
    ②当x=﹣2.1时，[x]+（x）+[x）=﹣7；
    ③方程4[x]+3（x）+[x）=11的解为1＜x＜1.5；
    ④当﹣1＜x＜1时，函数y=[x]+（x）+x的图象与正比例函数y=4x的图象有两个交点．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，给出以下四个结论：①abc=0，②a+b+c＞0，③a＞b，④4ac﹣b2＜0；其中正确的结论有（ ）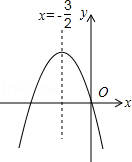
    A.1个
    B.2个
    C.3个
    D.4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠ACB=90°，AC=BC=4,CD⊥AB于D，P是线段CD上一个动点，以P为直角顶点向下作等腰Rt△BPE,连结AE,DE.

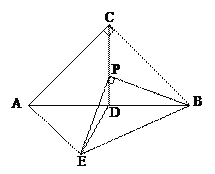
    (1)∠BAE的度数是否为定值？若是，求出∠BAE的度数；

    (2)直接写出DE的最小值。

    查看答案和解析>>

    同步练习册答案