
【题目】如图,在平面直角坐标系![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
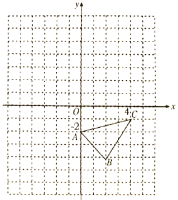
(1)请画出![]() 关于
关于![]() 轴对称的
轴对称的![]() (其中
(其中![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() ,
,![]() 的对称点,不写画法,写出
的对称点,不写画法,写出![]() 、
、![]() 、
、![]() 的坐标)
的坐标)
(2)在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使
,使![]() 的值最小,若有,请作出点
的值最小,若有,请作出点![]() ,并直接写出
,并直接写出![]() 点的坐标,若没有,请说明理由.
点的坐标,若没有,请说明理由.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
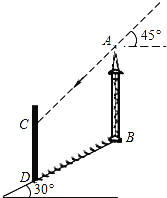
【题目】如图,在坡角为30°的山坡上有一铁塔AB,其正前方矗立着一大型广告牌,当阳光与水平线成45°角时,测得铁塔AB落在斜坡上的影子BD的长为6米,落在广告牌上的影子CD的长为4米,求铁塔AB的高(AB,CD均与水平面垂直,结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
如图1,点E.F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF、则EF=BE+DF,试说明理由;
(2)类比引申
如图2,在四边形ABCD中,AB=AD,∠BAD=90°,点E.F分别在边BC、CD上,∠EAF=45°,若∠B,∠D都不是直角,则当∠B与∠D满足等量关系 时,仍有EF=BE+DF;
(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°,猜想BD、DE、EC满足的等量关系,并写出推理过程。

查看答案和解析>>
科目:初中数学 来源: 题型:
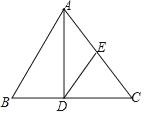
【题目】已知:如图,在△ABC中,AD是边BC上的高,E为边AC的中点,BC=21,AD=8,sinB=![]() .
.
求:(1)线段DC的长;
(2)tan∠EDC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=70°,∠BAC=30°,将△ABC绕点C顺时针旋转得到△EDC,当点B的对应点D恰好落在AC边上时,∠CAE的度数为___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具商店的某种毛笔每支售价25元,书法练习本每本售价5元,该商店为促销正在进行优惠活动:
活动1:买一支毛笔送一本书法练习本;
活动2:按购买金额的九折付款.
某学校准备为书法兴趣小组购买这种毛笔20支,书法练习本x(x≥20)本.
(1)写出两种优惠活动实际付款金额y1(元),y2(元)与x(本)之间的函数关系式;
(2)请问:该校选择哪种优惠活动更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
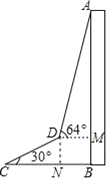
【题目】为了测量出大楼AB的高度,从距离楼底B处50米的点C(点C与楼底B在同一水平面上)出发,沿倾斜角为30°的斜坡CD前进20米到达点D,在点D处测得楼顶A的仰角为64°,求大楼AB的高度(结果精确到1米)(参考数据:sin64°≈0.9,cos64°≈0.4,tan64°≈2.1, ![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() .作DE⊥AC于点E,作AF⊥BD于点F.
.作DE⊥AC于点E,作AF⊥BD于点F.
(1)求AF、AE的长;
(2)若以点![]() 为圆心作圆,
为圆心作圆, ![]() 、
、![]() 、
、![]() 、E、F五点中至少有1个点在圆内,且至少有2个点在圆外,求
、E、F五点中至少有1个点在圆内,且至少有2个点在圆外,求![]() 的半径
的半径 ![]() 的取值范围.
的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com