Question

20．Rt△ABC中，∠ACB=90°，BC=4，如图1，点P从C出发向点B运动，点R是射线PB上一点，PR=3CP，过点R作QR⊥BC，且QR=aCP，连接PQ，当P点到达B点时停止运动．设CP=x，△ABC与△PQR重合部分的面积为S，S关于x的函数图象如图2所示（其中0＜x≤$\frac{3}{7}$，$\frac{3}{7}$＜x≤m，m＜x≤n时，函数的解析式不同）．
（1）a的值为4；
（2）求出S关于x的函数关系式，并写出x的取值范围．

Answer 1

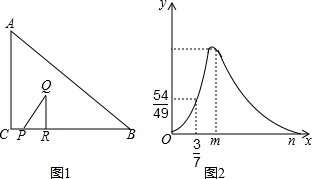
分析 （1）由图2可知当x=$\frac{3}{7}$时S=$\frac{54}{49}$，且此时Q点在线段AB上，利用三角形面积公式即可求出a的值；
（2）由Q点和R点的位置，可将整个移动过程分成三部分，借用三角形相似，找个各边的关系，分割图形，既能找出S和x之间的关系式．

解答 解：（1）由图2可知，当x=$\frac{3}{7}$时，点Q在线段AB上，且此时的S=$\frac{54}{49}$，
PR=3CP=$\frac{9}{7}$，QR=aCP=$\frac{3}{7}$a，
∵QR⊥BC，
∴S=$\frac{1}{2}$PR•QR=$\frac{1}{2}$×$\frac{9}{7}$×$\frac{3}{7}$a=$\frac{54}{49}$，即27a=108，
解得a=4．
故答案为4．
（2）当x=$\frac{3}{7}$时，Q点在线段AB上，如图3，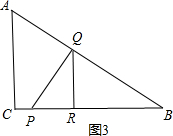

∵AC⊥BC，QR⊥BC，
∴AC∥QR，
∴△ABC∽△QBR，
∴$\frac{AC}{QR}$=$\frac{BC}{BR}$．
QR=4CP=$\frac{12}{7}$，PR=3CP=$\frac{9}{7}$，BR=BC-CP-PR=$\frac{16}{7}$，
AC=$\frac{BC}{BR}$•QR=$\frac{4}{\frac{16}{7}}$•$\frac{12}{7}$=3．
①当点Q在△ACB内时，即0＜x≤$\frac{3}{7}$时，如图1，
PR=3x，QR=4x，
S=$\frac{1}{2}$PR•QR=6x²．
②当点Q在△ACB外且R点在线段CB上时，如图4，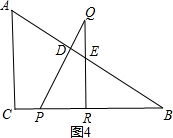

此时x＞$\frac{3}{7}$，且CR≤BC，
∵CR=CP+PR=4x，
∴$\frac{3}{7}$＜x≤1．
∵$\frac{PR}{QR}$=$\frac{3}{4}$=$\frac{AC}{BC}$，
∴△PQR∽△ABC，
∴∠Q=∠B，
∵∠DEQ=∠REB（对顶角），
∴△DEQ∽△REB．
在Rt△ACB中，由勾股定理可知AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=5，
∵AC∥QR，
∴△EBR∽△ABC，
∴$\frac{RE}{AC}$=$\frac{RB}{BC}$，
RB=BC-CP-PR=4-4x，AC=3，BC=4，
∴RE=3-3x．
QE=QR-RE=4x-（3-3x）=7x-3．
∵△DEQ∽△REB，△EBR∽△ABC，且AC=3，BC=4，AB=5，
∴DE=$\frac{3}{5}$QE，QD=$\frac{4}{5}$QE，QD⊥DE．
S=$\frac{1}{2}$PR•QR-$\frac{1}{2}$QD•DE=-$\frac{144}{25}$x²+$\frac{252}{25}$x-$\frac{54}{25}$．
③当点R在线段CB的延长线上时，如图5，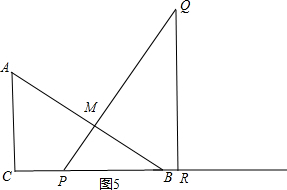

此时CR=4x＞BC=4，得x＞1；CP=x≤BC=4．
即1＜x≤4．
∵△ABC∽△PQR，
∴∠QPR=∠A，
∵∠PBM=∠ABC，
∴△PBM∽△ABC，
∴PM=$\frac{3}{5}$PB，MB=$\frac{4}{5}$PB．
∵PB=BC-CP=4-x，
∴S=$\frac{1}{2}$PM•MB=$\frac{6}{25}$（4-x）²=$\frac{6}{25}$x²-$\frac{48}{25}$x+$\frac{96}{25}$．
综合①②③可得：S=$\left\{\begin{array}{l}{6{x}^{2}（0＜x≤\frac{3}{4}）}\\{-\frac{144}{25}{x}^{2}+\frac{252}{25}x-\frac{54}{25}（\frac{3}{7}＜x≤1）}\\{\frac{6}{25}{x}^{2}-\frac{48}{25}x+\frac{96}{25}（1＜x≤4）}\end{array}\right.$．

点评 本题考查了动点问题的函数图象，解题的关键是：（1）由图2找出S的面积，套入三角形面积公式；（2）画出图形，结合三角形相似，找到边角关系，分割图形即可．