
【题目】已知在□ABCD中,AEBC于E,DF平分ADC 交线段AE于F.
(1)如图1,若AE=AD,ADC=60, 请直接写出线段CD与AF+BE之间所满足的等量关系;
(2)如图2, 若AE=AD,你在(1)中得到的结论是否仍然成立, 若成立,对你的结论加以证明, 若不成立, 请说明理由;
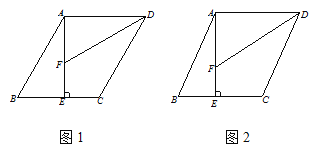
【答案】(1)CD=AF+BE.(2)(1)中的结论仍然成立.证明见解析.
【解析】试题分析:(1)、利用截长补短法可以得出线段之间的关系;(2)、延长EA到G,使得AG=BE,连结DG,根据平行四边形的性质得出△ABE和△DAG全等,从而得出DG=AB,根据角度之间的关系得出DG=GF,即CD=GF=AF+AG=AF+BE得出答案.
试题解析:(1)、CD=AF+BE.
(2)、解:(1)中的结论仍然成立.
证明:延长EA到G,使得AG=BE,连结DG,
∵ 四边形ABCD是平行四边形, ∴ AB=CD,AB∥CD,AD=BC,
∵ AE⊥BC于点E, ∴ ∠AEB=∠AEC=90, ∴∠AEB=∠DAG=90, ∴ ∠DAG=90,
∵ AE=AD, ∴ △ABE≌△DAG, ∴∠1=∠2, DG=AB, ∴∠GFD=90-∠3,
∵ DF平分∠ADC, ∴∠3=∠4,
∴∠GDF=∠2+∠3=∠1+∠4=180-∠FAD-∠3=90-∠3, ∴∠GDF=∠GFD,∴ DG=GF.
∴ CD=GF=AF+AG= AF + BE, 即 CD = AF +BE.


科目:初中数学 来源: 题型:
【题目】如图,东湖隧道的截面由抛物线和长方形构成,长方形的长OA为12cm,宽OB为4cm,隧道顶端D到路面的距离为10cm,建立如图所示的直角坐标系 
(1)求该抛物线的解析式.
(2)一辆货运汽车载一长方体集装箱,集装箱最高处与地面距离为6m,宽为4m,隧道内设双向行车道,问这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面高度相等,如果灯离地面的高度不超过8.5m,那么两排灯的水平距离最小是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大楼外墙有高为AB的广告牌,由距离大楼20米的点C(即CD=20米)观察它的顶部A的仰角是55°,底部B的仰角是42°,求AB的高度.(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43,sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+2与直线l交于点A、B两点,且A点为抛物线与y轴的交点,B(﹣2,﹣4),抛物线的对称轴是直线x=2,过点A作AC⊥AB,交抛物线于点C、x轴于点D.
(1)求此抛物线的解析式;
(2)求点D的坐标;
(3)抛物线上是否存在点K,使得以AC为边的平行四边形ACKL的面积等于△ABC的面积?若存在,请直接写出点K的横坐标;若不存在,请说明理由.[提示:抛物线y=ax2+bx+c(a≠0)的对称轴为x=﹣ ![]() ,顶点坐标为(﹣
,顶点坐标为(﹣ ![]() ,
, ![]() )].
)].
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,试判断BE与CF的位置关系,并说明你的理由.请补全下列说理过程.
,试判断BE与CF的位置关系,并说明你的理由.请补全下列说理过程.

解:BE ______ CF.
理由是:![]() 已知
已知![]() .
.
![]() ______
______ ![]() ______
______ ![]() 垂直的定义
垂直的定义![]()
![]() 已知
已知![]() .
.
![]() =______
=______ ![]() .(等式的基本性质)
.(等式的基本性质)
即![]() ______
______
![]() ______
______ ![]() ( ______________________
( ______________________ ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲口袋中装有3个相同的小球,它们分别写有数值﹣1,1,5;乙口袋中装有3个相同的小球,它们分别写有数值﹣4,2,3.现从甲口袋中随机取一球,记它上面的数值为x,再从乙口袋中随机取一球,记它上面的数值为y.设点A的坐标为(x,y),请用树形图或列表法,求点A落在第一象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接郑州市第二届“市长杯”青少年校园足球超级联赛,某学校组织了一次体育知识竞赛.每班选25名同学参加比赛,成绩分别为A、B、C、D四个等级,其中相应等级得分依次记为100分、90分、80分、70分.学校将八年级一班和二班的成绩整理并绘制成统计图,如图所示.
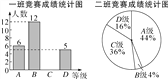
(1)把一班竞赛成绩统计图补充完整;
(2)写出下表中a、b、c的值:
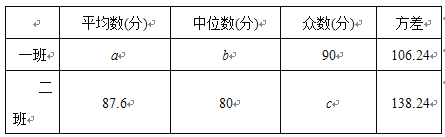
(3)根据(2)的结果,请你对这次竞赛成绩的结果进行分析.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、C、D都在半径为6的⊙O上,过点C作AC∥BD交OB的延长线于点A,连接CD,已知∠CDB=∠OBD=30°. 
(1)求证:AC是⊙O的切线;
(2)求弦BD的长;
(3)求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,将△ABC沿直线MN翻折后,顶点C恰好落在AB边上的点D处,已知MN∥AB,MC=6,NC= ![]() ,则四边形MABN的面积是( )
,则四边形MABN的面积是( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com