
| 距离地面高度h/km | 0 | 1 | 2 | 3 | 4 | 5 | … |
| 温度T/℃ | 20 | 14 | 8 | 2 | -4 | -10 | … |
分析 (1)直接利用表格中数据得出温度与高度之间的关系;
(2)利用(1)中所求,进而代入h的值求出答案;
(3)利用(1)中所求,进而代入T的值求出答案.
解答 解:(1)由表格中数据可得:
距离地面高度每升高1km,温度就降低6℃,进而猜想:温度T与距离地面高度h之间的函数关系式为:T=20-6h;
故答案为:6,T=20-6h;
(2)由(1)得:T=20-6×10=-40(℃),
答:当h=10km时,高空的温度T是-40℃;
(3)当T=-28℃时,则:-28=20-6h,
解得:h=8,
答:距离地面的高度h是8km.
点评 此题主要考查了函数关系式以及函数值,正确得出函数关系式是解题关键.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:填空题
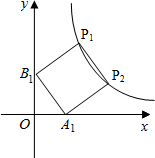 如图,正方形A1B1P1P2顶点P1、P2在反比例函数y=$\frac{2}{x}$(x>0)的图象上,顶点A1、B1分别在x轴、y轴的正半轴上,则点P2的坐标为(2,1).
如图,正方形A1B1P1P2顶点P1、P2在反比例函数y=$\frac{2}{x}$(x>0)的图象上,顶点A1、B1分别在x轴、y轴的正半轴上,则点P2的坐标为(2,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
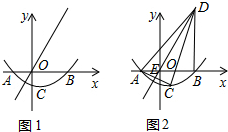
 如图,正方形A1A2A3A4,A5A6A7A8,A9A10A11A12,…,(每个正方形从第三象限的顶点开始,按顺时针方向顺序,依次记为A1,A2,A3,A4;A5,A6,A7,A8;A9,A10,A11,A12;…)的中心均在坐标原点O,各边均与x轴或y轴平行,若它们的边长依次是2,4,6…,则顶点A2015的坐标为(504,504).
如图,正方形A1A2A3A4,A5A6A7A8,A9A10A11A12,…,(每个正方形从第三象限的顶点开始,按顺时针方向顺序,依次记为A1,A2,A3,A4;A5,A6,A7,A8;A9,A10,A11,A12;…)的中心均在坐标原点O,各边均与x轴或y轴平行,若它们的边长依次是2,4,6…,则顶点A2015的坐标为(504,504).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
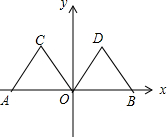 如图,在平面直角坐标系中,点A的坐标为(-2,0),等边△AOC经过平移或轴对称或旋转都可以得到△OBD.
如图,在平面直角坐标系中,点A的坐标为(-2,0),等边△AOC经过平移或轴对称或旋转都可以得到△OBD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com