练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    16．求抛物线y=x2-5x+4上纵坐标为4的点的坐标．

    分析 在二次函数中令y=4求x即可．

    解答 解：
    在y=x2-5x+4中，
    令y=4可得4=x2-5x+4，
    解得x=0或x=5，
    ∴抛物线y=x2-5x+4上纵坐标为4的点的坐标为（0，4）或（5，4）．

    点评 本题主要考查二次函数图象上点的坐标特征，掌握函数图象上点的坐标满足函数解析式是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

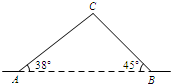    6．如图，从A地到B地的公路需经过C地，AC=10千米，∠CAB=38°，∠ABC=45°．因城市规划的需要，将在A、B两地之间修建一条笔直的公路．求改直后的公路AB的长（精确到1千米）．（参考数据：sin38°=0.62，cos38°=0.79，tan38°=0.78）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．如图所示的圆锥，它的主视图和俯视图分别是（　　）
    A．等边三角形、圆B．等边三角形、等腰三角形
    C．等腰三角形、圆D．圆、等腰三角形

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．如果a+b+c=0，那么一元二次方程ax2+bx+c=0必有一个根是1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

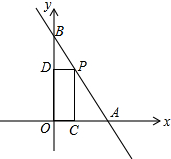    11．如图，一次函数y=-$\sqrt{3}$x+2$\sqrt{3}$的图象交x轴于点A，交y轴于点B，点P在线段AB上（不与点A、B重合），过点P分别作OA和OB的垂线，垂足分别为C、D．
    ①点A坐标为（2，0），线段AB=4；
    ②当矩形OCPD的面积为$\frac{3}{4}$$\sqrt{3}$时，求P点的坐标．
    ③连接CD，当线段CD的长为最小时，求点P坐标，并求CD的最小值为多少？
    ④平面直角坐标系内，是否存在点M，使得点A，P，O，M为顶点的四边形为菱形？若存在，直接写出点M的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．已知：x=$\frac{1}{\sqrt{2}-1}$，y=$\frac{1}{\sqrt{2}+1}$，求下列各式的值：
    （1）x2+2xy+y2；
    （2）x2-y2；
    （3）x2+y2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．计算：（-3$\frac{1}{5}$）×（-$\frac{2}{7}$）÷（+1$\frac{3}{5}$）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．计算：
    （1）（-1）100×5+（-2）4÷4                             
    （2）（-10）3+[（-4）2-（1-32）×2]．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．如图，在△ABC中，AB=AC=10，BC=12，I为△ABC的内心．
    （1）求S△ABC；
    （2）求BI的长．

    查看答案和解析>>

    同步练习册答案