
ЁОЬтФПЁПФГЬЈЛњДВЩњВњж§МўВњЦЗЃЌАДееЩњВњБъзМЃЌж§МўВњЦЗЦРЖЈЕШМЖЁЂећИФЗбгУЙцЖЈШчЯТЃК
жиСП ЃЈЕЅЮЛЃК | ЦРЖЈЕШМЖ | ећИФЗбгУ ЃЈЕЅЮЛЃКдЊ/МўЃЉ |
| ЬигХЦЗ | |
| гХЕШЦЗ | |
| КЯИёЦЗ | |
| ВЛКЯИёЦЗ | 50 |
| ВЛКЯИёЦЗ | 30 |
зЂЃКдкЭГМЦгХЕШЦЗИіЪ§ЪБЃЌНЋЬигХЦЗМЦЫудкФкЃЛдкЭГМЦКЯИёЦЗИіЪ§ЪБЃЌНЋгХЕШЦЗЃЈКЌЬигХЦЗЃЉМЦЫудкФк.
ЯжИУЛњДВЩњВњ20МўВњЦЗЃЌВтСПЦфжиСПЃЌЕУЕНШчЯТЭГМЦБэЃК
жиСП ЃЈЕЅЮЛЃК |
| 29.8 | 29.9 | 30.0 | 30.1 | 30.2 |
|
МўЪ§ | 2 | 3 | 4 |
| 3 | 1 |
|
ЖдееЩњВњБъзМЃЌЗЂЯжетХњж§МўВњЦЗЕФКЯИёТЪЮЊ![]() .
.
ЃЈ1ЃЉЧѓ![]() гы
гы![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉИљОнПЭЛЇвЊЧѓЃЌетХњж§МўВњЦЗЕФКЯИёТЪВЛЕУЕЭгк![]() .ЯжОіЖЈДгВЛКЯИёВњЦЗжаЫцЛњГщШЁСНМўНјааећИФЃЌЧѓећИФЗбгУзюЕЭЕФИХТЪ.
.ЯжОіЖЈДгВЛКЯИёВњЦЗжаЫцЛњГщШЁСНМўНјааећИФЃЌЧѓећИФЗбгУзюЕЭЕФИХТЪ.
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЌ
ЃЌ![]() .ЃЈ2ЃЉ
.ЃЈ2ЃЉ![]() ЃЈећИФЗбгУзюЕЭЃЉ
ЃЈећИФЗбгУзюЕЭЃЉ![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЭГМЦБэжаЕФВњЦЗКЯИёЕФМўЪ§НсКЯВњЦЗЕФКЯИёТЪПЩЕУГіxЕФжЕЃЌНјЖјПЩЕУГіyЕФжЕЃЛ
ЃЈ2ЃЉРћгУСаБэЗЈЛђЛЪїзДЭМЗЈРДЧѓНтМДПЩЃЎ
НтЗЈвЛЃКЃЈ1ЃЉгЩЬтвтЕУЃК![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЎ
ЃЎ
Ёр![]() ЃЎ
ЃЎ
ЃЈ2ЃЉМЧЁАжиСПаЁгкЛђЕШгк![]() ЁБЕФСНМўВњЦЗЮЊ
ЁБЕФСНМўВњЦЗЮЊ![]() ЁЂ
ЁЂ![]() ЃЌ
ЃЌ
МЧЁАжиСПДѓгкЛђЕШгк![]() ЁБЕФСНМўВњЦЗЮЊ
ЁБЕФСНМўВњЦЗЮЊ![]() ЁЂ
ЁЂ![]() ЃЎ
ЃЎ
ЛЪїзДЭМШчЯТЃК
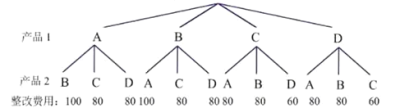
ЫљгаЛњЛсОљЕШЕФНсЙћга12жжЃЌЦфжаећИФЗбгУзюЕЭЕФНсЙћга2жжЃЌ
Ёр![]() ЃЈећИФЗбгУзюЕЭЃЉ
ЃЈећИФЗбгУзюЕЭЃЉ![]() ЃЎ
ЃЎ
НтЗЈЖўЃКЃЈ1ЃЉЭЌНтЗЈвЛЃК
ЃЈ2ЃЉМЧЁАжиСПаЁгкЛђЕШгк![]() ЁБЕФСНМўВњЦЗЮЊ
ЁБЕФСНМўВњЦЗЮЊ![]() ЁЂ
ЁЂ![]() ЃЌ
ЃЌ
МЧЁАжиСПДѓгкЛђЕШгк![]() ЁБЕФСНМўВњЦЗЮЊ
ЁБЕФСНМўВњЦЗЮЊ![]() ЁЂ
ЁЂ![]() ЃЎ
ЃЎ
СаБэШчЯТЃК
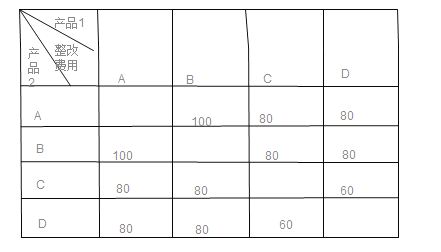
ЫљгаЛњЛсОљЕШЕФНсЙћга12жжЃЌЦфжаећИФЗбгУзюЕЭЕФНсЙћга2жжЃЌ
ЁрЃЈ![]() ЃЈећИФЗбгУзюЕЭЃЉ
ЃЈећИФЗбгУзюЕЭЃЉ![]() ЃЎ
ЃЎ


 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮвУЧЙцЖЈЃКШ§НЧаЮШЮвтСНБпЕФЁАМЋЛЏжЕЁБЕШгкЕкШ§БпЩЯЕФжаЯпКЭетБпвЛАыЕФЦНЗНВюЃЎШчЭМ1ЃЌдкЁїABCжаЃЌAOЪЧBCБпЩЯЕФжаЯпЃЌABгыACЕФЁАМЋЛЏжЕЁБОЭЕШгкAO2ЉBO2ЕФжЕЃЌПЩМЧЮЊABЁїAC=AO2ЉBO2ЃЎ
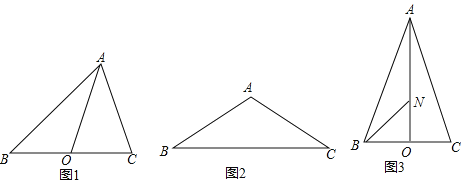
ЃЈ1ЃЉдкЭМ1жаЃЌШєЁЯBAC=90ЁуЃЌAB=8ЃЌAC=6ЃЌAOЪЧBCБпЩЯЕФжаЯпЃЌдђABЁїAC= ЃЌOCЁїOA= ЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌдкЁїABCжаЃЌAB=AC=4ЃЌЁЯBAC=120ЁуЃЌЧѓABЁїACЁЂBAЁїBCЕФжЕЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌдкЁїABCжаЃЌAB=ACЃЌAOЪЧBCБпЩЯЕФжаЯпЃЌЕуNдкAOЩЯЃЌЧвON=![]() AOЃЎвбжЊABЁїAC=14ЃЌBNЁїBA=10ЃЌЧѓЁїABCЕФУцЛ§ЃЎ
AOЃЎвбжЊABЁїAC=14ЃЌBNЁїBA=10ЃЌЧѓЁїABCЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌОиаЮгВжНЦЌABCDЕФЖЅЕуAдк![]() жсЕФе§АыжсМАдЕуЩЯЛЌЖЏЃЌЖЅЕуBдк
жсЕФе§АыжсМАдЕуЩЯЛЌЖЏЃЌЖЅЕуBдк![]() жсЕФе§АыжсМАдЕуЩЯЛЌЖЏЃЌЕуEЮЊABЕФжаЕуЃЌAB=24,BC=5,ИјГіЯТСаНсТлЃКЂйЕуAДгЕуOГіЗЂЃЌЕНЕуBдЫЖЏжСЕуOЮЊжЙЃЌЕуEОЙ§ЕФТЗОЖГЄЮЊ12ІаЃЛЂкЁїOABЕФУцЛ§ЕФзюДѓжЕЮЊ144ЃЛЂлЕБODзюДѓЪБЃЌЕуDЕФзјБъЮЊ
жсЕФе§АыжсМАдЕуЩЯЛЌЖЏЃЌЕуEЮЊABЕФжаЕуЃЌAB=24,BC=5,ИјГіЯТСаНсТлЃКЂйЕуAДгЕуOГіЗЂЃЌЕНЕуBдЫЖЏжСЕуOЮЊжЙЃЌЕуEОЙ§ЕФТЗОЖГЄЮЊ12ІаЃЛЂкЁїOABЕФУцЛ§ЕФзюДѓжЕЮЊ144ЃЛЂлЕБODзюДѓЪБЃЌЕуDЕФзјБъЮЊ![]() ЃЌЦфжае§ШЗЕФНсТлЪЧ_________ЃЈЬюаДађКХЃЉ.
ЃЌЦфжае§ШЗЕФНсТлЪЧ_________ЃЈЬюаДађКХЃЉ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌДгЕуAПДвЛЩНЦТЩЯЕФЕчЯпИЫPQЃЌЙлВтЕуPЕФбіНЧЪЧ45ЁуЃЌЯђЧАзп6mЕНДяBЕуЃЌВтЕУЖЅЖЫЕуPКЭИЫЕзЖЫЕуQЕФбіНЧЗжБ№ЪЧ60ЁуКЭ30ЁуЃЌдђИУЕчЯпИЫPQЕФИпЖШЃЈЁЁЁЁЃЉ
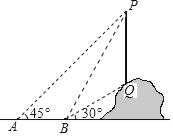
A. 6+2![]() B. 6+
B. 6+![]() C. 10Љ
C. 10Љ![]() D. 8+
D. 8+![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬЕъОЯњвЛжжбЇЩњгУЫЋМчАќЃЌвбжЊетжжЫЋМчАќЕФГЩБОМлЮЊУПИі30дЊЃЌЪаГЁЕїВщЗЂЯжЃЌетжжЫЋМчАќУПЬьЕФЯњЪлСП(Иі)гыyЯњЪлЕЅМлx(дЊ)гаШчЯТЙиЯЕ:![]() ЃЌЩшетжжЫЋМчАќУПЬьЕФЯњЪлРћШѓЮЊwдЊЃЎ
ЃЌЩшетжжЫЋМчАќУПЬьЕФЯњЪлРћШѓЮЊwдЊЃЎ
(1)етжжЫЋМчАќЯњЪлЕЅМлЖЈЮЊЖрЩйдЊЪБЃЌУПЬьЕФЯњЪлРћШѓзюДѓ?зюДѓРћШѓЪЧЖрЩйдЊ?
(2)ШчЙћЮяМлВПУХЙцЖЈетжжЫЋМчАќЕФЯњЪлЕЅМлВЛИпгк42дЊЃЌИУЩЬЕъЯњЪлетжжЫЋМчАќУПЬьвЊЛёЕУ200дЊЕФЯњЪлРћШѓЃЌЯњЪлЕЅМлгІЖЈЮЊЖрЩйдЊ?
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊRtЁїABCжаЃЌЁЯCЃН90ЁуЃЌADЪЧЁЯBACЕФНЧЦНЗжЯпЃЎ
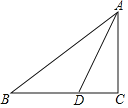
ЃЈ1ЃЉЧыГпЙцзїЭМЃКзїЁбOЃЌЪЙдВаФOдкABЩЯЃЌЧвADЮЊЁбOЕФвЛЬѕЯвЃЎЃЈВЛаДзїЗЈЃЌБЃСєзїЭМКлМЃЃЉЃЛ
ЃЈ2ЃЉХаЖЯжБЯпBCгыЫљзїЁбOЕФЮЛжУЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЬьУЈЩЬГЧФГЭјЕъЯњЪлФГПюРЖбРЖњЛњЃЌНјМлЮЊ100дЊ![]() дкдЊЕЉМДНЋРДСйжЎМЪЃЌПЊеЙСЫЪаГЁЕїВщЃЌЕБРЖбРЖњЛњЯњЪлЕЅМлЪЧ180дЊЪБЃЌЦНОљУПдТЕФЯњЪлСПЪЧ200МўЃЌШєЯњЪлЕЅМлУПНЕЕЭ2дЊЃЌЦНОљУПдТОЭПЩвдЖрЪлГі10МўЃЎ
дкдЊЕЉМДНЋРДСйжЎМЪЃЌПЊеЙСЫЪаГЁЕїВщЃЌЕБРЖбРЖњЛњЯњЪлЕЅМлЪЧ180дЊЪБЃЌЦНОљУПдТЕФЯњЪлСПЪЧ200МўЃЌШєЯњЪлЕЅМлУПНЕЕЭ2дЊЃЌЦНОљУПдТОЭПЩвдЖрЪлГі10МўЃЎ
![]() ЩшУПМўЩЬЦЗНЕМлxдЊЃЌИУЭјЕъЦНОљУПдТЛёЕУЕФРћШѓЮЊyдЊЃЌЧыаДГіyгыxдЊжЎМфЕФКЏЪ§ЙиЯЕЃЛ
ЩшУПМўЩЬЦЗНЕМлxдЊЃЌИУЭјЕъЦНОљУПдТЛёЕУЕФРћШѓЮЊyдЊЃЌЧыаДГіyгыxдЊжЎМфЕФКЏЪ§ЙиЯЕЃЛ
![]() ИУЭјЕъгІИУШчКЮЖЈМлВХФмЪЙЕУЦНОљУПдТЛёЕУЕФРћШѓзюДѓЃЌзюДѓРћШѓЪЧЖрЩйдЊЃП
ИУЭјЕъгІИУШчКЮЖЈМлВХФмЪЙЕУЦНОљУПдТЛёЕУЕФРћШѓзюДѓЃЌзюДѓРћШѓЪЧЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌАбСтаЮ![]() ЯђгвЦНвЦжС
ЯђгвЦНвЦжС![]() ЕФЮЛжУЃЌзї
ЕФЮЛжУЃЌзї![]() ЃЌДЙзуЮЊ
ЃЌДЙзуЮЊ![]() ЃЌ
ЃЌ![]() гы
гы![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌ
ЃЌ![]() ЕФбгГЄЯпНЛ
ЕФбгГЄЯпНЛ![]() гкЕу
гкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌдђЯТСаНсТлЃК
ЃЌдђЯТСаНсТлЃК
Ђй![]() ЃЛЂк
ЃЛЂк![]() ЃЛЂл
ЃЛЂл![]() ЃКЂм
ЃКЂм![]() .
.
дђЦфжаЫљгаГЩСЂЕФНсТлЪЧЃЈ ЃЉ
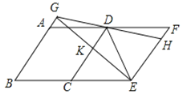
A.ЂйЂкЂлЂмB.ЂйЂкЂмC.ЂкЂлЂмD.ЂйЂл
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯп![]() ЕФЖЅЕузјБъЮЊ
ЕФЖЅЕузјБъЮЊ![]() ЃЌгы
ЃЌгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌгы
ЃЌгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌ
ЃЌ![]() .
.

ЃЈ1ЃЉЧѓЖўДЮКЏЪ§![]() ЕФБэДяЪНЃЛ
ЕФБэДяЪНЃЛ
ЃЈ2ЃЉЙ§Еу![]() зї
зї![]() ЦНаагк
ЦНаагк![]() жсЃЌНЛХзЮяЯпгкЕу
жсЃЌНЛХзЮяЯпгкЕу![]() ЃЌЕу
ЃЌЕу![]() ЮЊХзЮяЯпЩЯЕФвЛЕуЃЈЕу
ЮЊХзЮяЯпЩЯЕФвЛЕуЃЈЕу![]() дк
дк![]() ЩЯЗНЃЉЃЌзї
ЩЯЗНЃЉЃЌзї![]() ЦНаагк
ЦНаагк![]() жсНЛ
жсНЛ![]() гкЕу
гкЕу![]() ЃЌЕБЕу
ЃЌЕБЕу![]() дкКЮЮЛжУЪБЃЌЫФБпаЮ
дкКЮЮЛжУЪБЃЌЫФБпаЮ![]() ЕФУцЛ§зюДѓЃПВЂЧѓГізюДѓУцЛ§.
ЕФУцЛ§зюДѓЃПВЂЧѓГізюДѓУцЛ§.
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com