
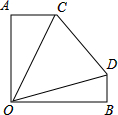
 如图,A在O的正北方向,B在O的正东方向,且OA=OB.某一时刻,甲车从A出发,以60km/h的速度朝正东方向行驶,与此同时,乙车从B出发,以40km/h的速度朝正北方向行驶.1小时后,位于点O处的观察员发现甲、乙两车之间的夹角为45°,即∠COD=45°,此时,甲、乙两人相距的距离为( )
如图,A在O的正北方向,B在O的正东方向,且OA=OB.某一时刻,甲车从A出发,以60km/h的速度朝正东方向行驶,与此同时,乙车从B出发,以40km/h的速度朝正北方向行驶.1小时后,位于点O处的观察员发现甲、乙两车之间的夹角为45°,即∠COD=45°,此时,甲、乙两人相距的距离为( )| A. | 90km | B. | 50$\sqrt{2}$km | C. | 20$\sqrt{13}$km | D. | 100km |
分析 根据旋转的性质结合全等三角形的判定与性质得出△COD≌△B′OC(SAS),则B′C=DC进而求出即可.
解答 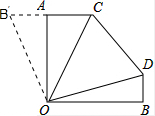 解:由题意可得:AB′=BD=40km,AC=60km,
解:由题意可得:AB′=BD=40km,AC=60km,
将△OBD顺时针旋转270°,则BO与AO重合,
在△COD和△B′OC中,
∵$\left\{\begin{array}{l}{DO={OB}^{′}}\\{∠COD=∠{B}^{′}OC}\\{CO=CO}\end{array}\right.$,
∴△COD≌△B′OC(SAS),
∴B′C=DC=40+60=100(km),
∴甲、乙两人相距的距离为100km;
故选:D.
点评 此题主要考查了解直角三角形的应用,用到的知识点是勾股定理的应用以及全等三角形的判定与性质,根据题意得出△COD≌△B′OC是解题关键.


科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,直线y=mx+1与双曲y=$\frac{k}{x}$(k>0)相交于点A、B,点C在x轴正半轴上,点D(1,-2),连结OA、OD、DC、AC,四边形AODC为菱形.
如图,在平面直角坐标系xOy中,直线y=mx+1与双曲y=$\frac{k}{x}$(k>0)相交于点A、B,点C在x轴正半轴上,点D(1,-2),连结OA、OD、DC、AC,四边形AODC为菱形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,已知线段MN,若用尺规作图作出MN的中点O,然后再取OM的中点A,然后分别以O、A为圆心,以OM长为半径画弧,两弧交于点B,测量∠MBN的度数,结果为( )
如图所示,已知线段MN,若用尺规作图作出MN的中点O,然后再取OM的中点A,然后分别以O、A为圆心,以OM长为半径画弧,两弧交于点B,测量∠MBN的度数,结果为( )| A. | 70° | B. | 80° | C. | 90° | D. | 100° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
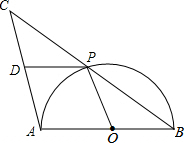 如图,AB是半圆O的直径,点P是半圆上不与点A、B重合的一个动点,延长BP到点C,使PC=PB,D是AC的中点,连接PD、PO.
如图,AB是半圆O的直径,点P是半圆上不与点A、B重合的一个动点,延长BP到点C,使PC=PB,D是AC的中点,连接PD、PO.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
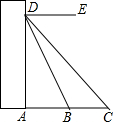 如图,小明家所在住宅楼楼前广场的宽AB为30米,线段BC为AB正前方的一条道路的宽.小明站在家里点D处观察B,C两点的俯角分别为60°和45°,已知DA垂直地面,则这条道路的宽BC为21.96米($\sqrt{3}$≈1.732)
如图,小明家所在住宅楼楼前广场的宽AB为30米,线段BC为AB正前方的一条道路的宽.小明站在家里点D处观察B,C两点的俯角分别为60°和45°,已知DA垂直地面,则这条道路的宽BC为21.96米($\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | ±1 | D. | 0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com