
ЁОЬтФПЁПЮвУЧжЊЕРЦНааЫФБпаЮгаКмЖраджЪЃЌЯждкШчЙћЮвУЧАбЦНааЫФБпаЮбизХЫќЕФвЛЬѕЖдНЧЯпЗелЃЌЛсЗЂЯжетЦфжаЛЙгаИќЖрЕФНсТлЃЎ
ЃЈЗЂЯжНсТлЃЉ
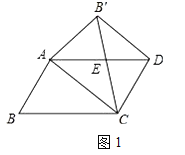
ЃЈ1ЃЉШчЭМЃЌдкЁѕABCDжаЃЌABЁйBCЃЌНЋЁїABCбиACЗелжСЁїABЁфCЃЌСЌНсBЁфDЃЌЗЂЯжСНИігаШЄЕФНсТлЃКЂйЁїEACЪЧЕШбќШ§НЧаЮ ЂкAC//BЁфD ЧыФубЁдёЦфжавЛИіНсТлМгвджЄУї
ЃЈНсТлдЫгУЃЉ
ЃЈ2ЃЉдкЁѕABCDжаЃЌвбжЊЃКBC=2ЃЌЁЯB=60ЁуЃЌНЋЁїABCбиACЗелжСЁїABЁфCЃЌСЌНсBЁфDЃЈШчЩЯЭМЃЉЃЎШєЫФБпаЮACDBЁфЪЧОиаЮЃЌЧѓACЕФГЄЃЎ
ЃЈЗНЗЈЭиеЙЃЉ
ЃЈ3ЃЉШє ![]() =kЃЌЧввдAЁЂCЁЂDЁЂBЁфЮЊЖЅЕуЕФЫФБпаЮЮЊе§ЗНаЮЃЌдђkЕФжЕЮЊ ЃЎ
=kЃЌЧввдAЁЂCЁЂDЁЂBЁфЮЊЖЅЕуЕФЫФБпаЮЮЊе§ЗНаЮЃЌдђkЕФжЕЮЊ ЃЎ
ЁОД№АИЁПЃЈ1ЃЉжЄУїМћНтЮіЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉkЕФжЕЮЊ1Лђ
ЃЛЃЈ3ЃЉkЕФжЕЮЊ1Лђ![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉЂйгЩЦНааЫФБпаЮЕФаджЪЕУГіЁЯEACЃНЁЯACBЃЌгЩЗелЕФаджЪЕУГіЁЯACBЃНЁЯACBЁфЃЌжЄГіЁЯEACЃНЁЯACBЁфЃЌЕУГіAEЃНCEМДПЩЃЛЂкЭЌЂйжЄУїAEЃНCEЃЌШЛКѓЧѓГіDEЃНBЁфEЃЌжЄГіЁЯCBЁфDЃНЁЯBЁфDAЃЌгЩЁЯAECЃНЁЯBЁфEDЃЌЕУГіЁЯACBЁфЃНЁЯCBЁфDЃЌМДПЩЕУГіAC//BЁфDЃЛ
ЃЈ2ЃЉгЩОиаЮЕФаджЪПЩЕУЁЯBACЃН90ЁуЃЌШЛКѓРћгУКЌ30ЁужБНЧШ§НЧаЮЕФаджЪКЭЙДЙЩЖЈРэЧѓНтМДПЩЃЛ
ЃЈ3ЃЉЗжСНжжЧщПіЬжТлЃЌЗжБ№зїГіЭМаЮЃЌИљОнЕШбќжБНЧШ§НЧаЮЕФаджЪЧѓНтМДПЩ.
НтЃКЃЈ1ЃЉбЁНсТлЂйЃЌ
жЄУїЃКЁпЫФБпаЮABCDЪЧЦНааЫФБпаЮЃЌ
ЁрADЃНBCЃЌADЁЮBCЃЌ
ЁрЁЯEACЃНЁЯACBЃЌ
гЩЗелЕФаджЪЕУЃКЁЯACBЃНЁЯACBЁфЃЌBCЃНBЁфCЃЌ
ЁрЁЯEACЃНЁЯACBЁфЃЌ
ЁрAEЃНCEЃЌМДЁїACEЪЧЕШбќШ§НЧаЮЃЛ
бЁНсТлЂкЃЌ
жЄУїЃКЁпЫФБпаЮABCDЪЧЦНааЫФБпаЮЃЌ
ЁрADЃНBCЃЌADЁЮBCЃЌ
ЁрЁЯEACЃНЁЯACBЃЌ
гЩЗелЕФаджЪЕУЃКЁЯACBЃНЁЯACBЁфЃЌBCЃНBЁфCЃЌ
ЁрЁЯEACЃНЁЯACBЁфЃЌ
ЁрAEЃНCEЃЌ
ЁрDEЃНBЁфEЃЌ
ЁрЁЯCBЁфDЃНЁЯBЁфDAЃЌ
ЁпЁЯAECЃНЁЯBЁфEDЃЌ
ЁрЁЯACBЁфЃНЁЯCBЁфDЃЌ
ЁрAC//BЁфDЃЛ
ЃЈ2ЃЉШчЭМ1ЫљЪОЃК
ЁпЫФБпаЮACDBЁфЪЧОиаЮЃЌ
ЁрЁЯCABЁфЃН90ЁуЃЌ
ЁрЁЯBACЃН90ЁуЃЌ
ЁпЁЯBЃН60ЁуЃЌBC=2ЃЌ
ЁрABЃН1ЃЌ
Ёр![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЗжСНжжЧщПіЃК
ЂйШчЭМ2ЫљЪОЃЌ
ЁпЫФБпаЮACDBЁфЪЧе§ЗНаЮЃЌ
ЁрABЁфЃНACЃЌ
ЁпABЁфЃНABЃЌ
ЁрABЃНACЃЌМД![]() ЃЛ
ЃЛ
ЂкШчЭМ3ЫљЪОЃЌ
ЁпЫФБпаЮACBЁфDЪЧе§ЗНаЮЃЌ
ЁрЁЯABЁфBЃН45ЁуЃЌЁЯACBЁфЃН90ЁуЃЌ
ЁпABЁфЃНABЃЌ
ЁрЁЯBЃН45ЁуЃЌЁЯACBЃН90ЁуЃЌ
ЁрЁїABCЪЧЕШбќжБНЧШ§НЧаЮЃЌ
Ёр![]() ЃЌ
ЃЌ
злЩЯЫљЪіЃЌkЕФжЕЮЊ1Лђ![]() .
.



 ОйвЛЗДШ§ЭЌВНЧЩНВОЋСЗЯЕСаД№АИ
ОйвЛЗДШ§ЭЌВНЧЩНВОЋСЗЯЕСаД№АИ ПкЫугыгІгУЬтПЈЯЕСаД№АИ
ПкЫугыгІгУЬтПЈЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
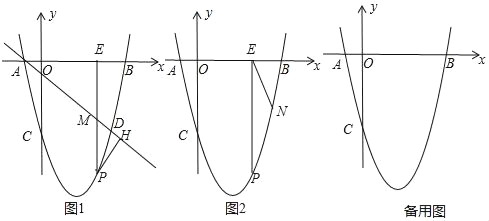
ЁОЬтФПЁПШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпy=ax2+bx+cЃЈaЁй0ЃЉгыxжсНЛгкAЃЌBСНЕуЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌгыyжсНЛгкЕуCЃЌЕуAЕФзјБъЮЊЃЈЉ1ЃЌ0ЃЉЃЌЧвOC=OBЃЌtanЁЯOAC=4ЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєЕуDКЭЕуCЙигкХзЮяЯпЕФЖдГЦжсЖдГЦЃЌжБЯпADЯТЗНЕФХзЮяЯпЩЯгавЛЕуPЃЌЙ§ЕуPзїPHЁЭADгкЕуHЃЌзїPMЦНаагкyжсНЛжБЯпADгкЕуMЃЌНЛxжсгкЕуEЃЌЧѓЁїPHMЕФжмГЄЕФзюДѓжЕЃЎ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌШчЭМ2ЃЌдкжБЯпEPЕФгвВрЁЂxжсЯТЗНЕФХзЮяЯпЩЯЪЧЗёДцдкЕуNЃЌЙ§ЕуNзїNGЁЭxжсНЛxжсгкЕуGЃЌЪЙЕУвдЕуEЁЂNЁЂGЮЊЖЅЕуЕФШ§НЧаЮгыЁїAOCЯрЫЦЃПШчЙћДцдкЃЌЧыжБНгаДГіЕуGЕФзјБъЃКШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖўДЮКЏЪ§y=ax2ЃЋbxЃЋcЭМЯѓЕФвЛВПЗжШчЭМЫљЪОЃЎвбжЊЫќЕФЖЅЕуMдкЕкЖўЯѓЯоЃЌЧвОЙ§ЕуA(1ЃЌ0)КЭЕуB(0ЃЌl)ЃЎШєДЫЖўДЮКЏЪ§ЕФЭМЯѓгыxжсЕФСэвЛИіНЛЕуЮЊC.
ЃЈ1ЃЉЪдЧѓaЃЌbЫљТњзуЕФЙиЯЕЪНЃЛ
ЃЈ2ЃЉЕБЁїAMCЕФУцЛ§ЮЊЁїABCУцЛ§ЕФ![]() БЖЪБЃЌЧѓaЕФжЕЃЛ
БЖЪБЃЌЧѓaЕФжЕЃЛ
ЃЈ3ЃЉЪЧЗёДцдкЪЕЪ§aЃЌЪЙЕУЁїABCЮЊжБНЧШ§НЧаЮЃЎШєДцдкЃЌЧыЧѓГіaЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁЁ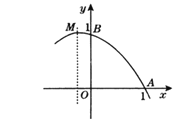
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
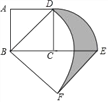
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮABCDжаЃЌAB=2ЃЌНЋЯпЖЮCDШЦЕуCЫГЪБеыа§зЊ90ЁуЕУЕНЯпЖЮCEЃЌЯпЖЮBDШЦЕуBЫГЪБеыа§зЊ90ЁуЕУЕНЯпЖЮBFЃЌСЌНгBFЃЌдђЭМжавѕгАВПЗжЕФУцЛ§ЪЧ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ2011ЩНЖЋМУФЯЃЌ27ЃЌ9ЗжЃЉШчЭМЃЌОиаЮOABCжаЃЌЕуOЮЊдЕуЃЌЕуAЕФзјБъЮЊЃЈ0ЃЌ8ЃЉЃЌЕуCЕФзјБъЮЊЃЈ6ЃЌ0ЃЉЃЎХзЮяЯп![]() ОЙ§AЁЂCСНЕуЃЌгыABБпНЛгкЕуDЃЎ
ОЙ§AЁЂCСНЕуЃЌгыABБпНЛгкЕуDЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉЕуPЮЊЯпЖЮBCЩЯвЛИіЖЏЕуЃЈВЛгыЕуCжиКЯЃЉЃЌЕуQЮЊЯпЖЮACЩЯвЛИіЖЏЕуЃЌAQ=CPЃЌСЌНгPQЃЌЩшCP=mЃЌЁїCPQЕФУцЛ§ЮЊSЃЎ
ЂйЧѓSЙигкmЕФКЏЪ§БэДяЪНЃЌВЂЧѓГіmЮЊКЮжЕЪБЃЌSШЁЕУзюДѓжЕЃЛ
ЂкЕБSзюДѓЪБЃЌдкХзЮяЯп![]() ЕФЖдГЦжсlЩЯШєДцдкЕуFЃЌЪЙЁїFDQЮЊжБНЧШ§НЧаЮЃЌЧыжБНгаДГіЫљгаЗћКЯЬѕМўЕФFЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФЖдГЦжсlЩЯШєДцдкЕуFЃЌЪЙЁїFDQЮЊжБНЧШ§НЧаЮЃЌЧыжБНгаДГіЫљгаЗћКЯЬѕМўЕФFЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
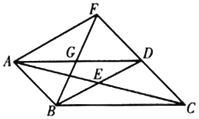
ЁОЬтФПЁПШчЭМЃЌвбжЊ![]() ЃЌ
ЃЌ![]() ЃЌАДШчЯТВНжшзїЭМЃК
ЃЌАДШчЯТВНжшзїЭМЃК
ЃЈ1ЃЉЗжБ№вд![]() ЁЂ
ЁЂ![]() ЮЊдВаФЃЌвдДѓгк
ЮЊдВаФЃЌвдДѓгк![]() ЕФГЄЮЊАыОЖдк
ЕФГЄЮЊАыОЖдк![]() СНБпзїЛЁЃЌНЛгкСНЕу
СНБпзїЛЁЃЌНЛгкСНЕу![]() ЁЂ
ЁЂ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉОЙ§![]() ЁЂ
ЁЂ![]() зїжБЯпЃЌЗжБ№НЛ
зїжБЯпЃЌЗжБ№НЛ![]() ЁЂ
ЁЂ![]() гкЕу
гкЕу![]() ЁЂ
ЁЂ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЙ§Еу![]() зї
зї![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЁЂ
ЁЂ![]() ЃЎ
ЃЎ
дђЯТСаНсТлЃКЂй![]() ЁЂ
ЁЂ![]() ДЙжБЦНЗж
ДЙжБЦНЗж![]() ЃЛЂк
ЃЛЂк![]() ЃЛЂл
ЃЛЂл![]() ЦНЗж
ЦНЗж![]() ЃЛЂмЫФБпаЮ
ЃЛЂмЫФБпаЮ![]() ЪЧСтаЮЃЛЂнЫФБпаЮ
ЪЧСтаЮЃЛЂнЫФБпаЮ![]() ЪЧСтаЮ.ЦфжавЛЖЈе§ШЗЕФЪЧ______ЃЈЬюађКХЃЉЃЎ
ЪЧСтаЮ.ЦфжавЛЖЈе§ШЗЕФЪЧ______ЃЈЬюађКХЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
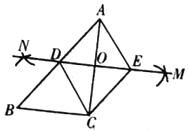
ЁОЬтФПЁПШчЭМЃЌЦНааЫФБпаЮ![]() ЕФЖдНЧЯп
ЕФЖдНЧЯп![]() гы
гы![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌЕу
ЃЌЕу![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌСЌНг
ЕФжаЕуЃЌСЌНг![]() ВЂбгГЄНЛ
ВЂбгГЄНЛ![]() ЕФбгГЄЯпгкЕу
ЕФбгГЄЯпгкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЕБ![]() ЃЌ
ЃЌ![]() ЪБЃЌЧыХаЖЯЫФБпаЮ
ЪБЃЌЧыХаЖЯЫФБпаЮ![]() ЕФаЮзДЃЌВЂжЄУїФуЕФНсТлЃЎ
ЕФаЮзДЃЌВЂжЄУїФуЕФНсТлЃЎ
ЃЈ3ЃЉЕБЫФБпаЮ![]() ЪЧе§ЗНаЮЪБЃЌЧыХаЖЯ
ЪЧе§ЗНаЮЪБЃЌЧыХаЖЯ![]() ЕФаЮзДЃЌВЂжЄУїФуЕФНсТлЃЎ
ЕФаЮзДЃЌВЂжЄУїФуЕФНсТлЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊОиаЮABCDЕФЖЅЕуAЁЂDЗжБ№ТфдкxжсЁЂyжсЃЌOD=2OA=6ЃЌADЃКAB=3ЃК1ЃЎдђЕуBЕФзјБъЪЧ_______ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌOPЦНЗжЁЯBOAЃЌPCЁЭOAЃЌPDЁЭOBЃЌДЙзуЗжБ№ЪЧCЁЂDЃЌдђЯТСаНсТлжаДэЮѓЕФЪЧЃЈЁЁЁЁЃЉ

A. PC=PD B. OC=OD C. OC=OP D. ЁЯCPO=ЁЯDPO
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com