
分析 直接运用:可以直接套用题意所给的结论,即可得出结果;
变形运用:先得出$\frac{{y}_{2}}{{y}_{1}}$的表达式,然后将(x+1)看做一个整体,继而再运用所给结论即可;
实际应用:用x表示出y,再套用题意所给的结论可求得答案.
解答 解:
直接应用:
∵函数y=x+$\frac{a}{x}$(a>0,x>0),由上述结论可知:当x=$\sqrt{a}$时,该函数有最小值为2$\sqrt{a}$.
∴函数y1=x(x>0)与函数y2=$\frac{1}{x}$(x>0),则当x=1时,y1+y2取得最小值为2.
故答案为:1,2;
变形应用:
已知函数y1=x+1(x>-1)与函数y2=(x+1)2+4(x>-1),
则$\frac{{y}_{2}}{{y}_{1}}$=$\frac{(x+1)^{2}+4}{x+1}$=(x+1)+$\frac{4}{x+1}$的最小值为:2×$\sqrt{4}$=4,
∵当(x+1)+$\frac{4}{x+1}$=4时,
整理得出:x2-2x+1=0,
解得:x1=x2=1,
检验:x=1时,x+1=2≠0,
故x=1是原方程的解,
故$\frac{{y}_{2}}{{y}_{1}}$的最小值为4,相应的x的值为1;
实际应用:
由池底宽为x(x>0)米,
由池底面积为4,得池底的长为$\frac{4}{x}$米,则y=480+320(x+$\frac{4}{x}$)(x>0),
∴水池的总造价y(元)与池底宽x(米)之间的函数关系式是 y=480+320(x+$\frac{4}{x}$),
∵(x+$\frac{4}{x}$)≥2×$\sqrt{4}$=4,
∴480+320(x+$\frac{4}{x}$)≥480+4×320=1760,
又由x+$\frac{4}{x}$=4可解得x=2,
∴当x为2米时,水池总造价y最低,最低是1760元.
点评 此题考查了反比例函数的应用及几何不等式的知识等知识,题目出的比较新颖,解答本题的关键是仔细审题,理解题意所给的结论,达到学以致用的目的.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,AC=BC,∠ACB=90°,点D为边AB上一点,CD绕点D顺时针旋转90°至DE,CE交AB于点G.已知AD=4,BG=3,点F是AE的中点,连接DF,求线段DF的长.
如图,在Rt△ABC中,AC=BC,∠ACB=90°,点D为边AB上一点,CD绕点D顺时针旋转90°至DE,CE交AB于点G.已知AD=4,BG=3,点F是AE的中点,连接DF,求线段DF的长.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 将正整数按如图所示规律排列下去,若用有序实数对(m,n)表示m排,从左到右第n个数,如(4,3)表示实数9,则(10,8)表示实数是53.
将正整数按如图所示规律排列下去,若用有序实数对(m,n)表示m排,从左到右第n个数,如(4,3)表示实数9,则(10,8)表示实数是53.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
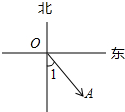 如图,O为我国南海某人造海岛,某国商船在A的位置,∠1=40°,下列说法正确的是( )
如图,O为我国南海某人造海岛,某国商船在A的位置,∠1=40°,下列说法正确的是( )| A. | 商船在海岛的北偏西50°方向 | B. | 海岛在商船的北偏西40°方向 | ||
| C. | 海岛在商船的东偏南50°方向 | D. | 商船在海岛的东偏南40°方向 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,∠ACB=90°,AC=5,BC=12,CO⊥AB于点O,D是线段OB上一点,DE=2,ED∥AC(∠ADE<90°),连接BE、CD.设BE、CD的中点分别为P、Q.
如图,△ABC中,∠ACB=90°,AC=5,BC=12,CO⊥AB于点O,D是线段OB上一点,DE=2,ED∥AC(∠ADE<90°),连接BE、CD.设BE、CD的中点分别为P、Q.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 延长射线AB到C,使BC=$\frac{1}{2}$AB | B. | 延长线段AB到C,使BC=$\frac{1}{2}$AB | ||
| C. | 反向延长线段AB到C,使BC=$\frac{1}{2}$AB | D. | 反向延长射线AB到C,使BC=$\frac{1}{2}$AB |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com