
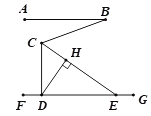
【题目】如图,直线AB∥FG,CE平分∠BCD,交FG于点E,过点D作DH⊥CE,垂足为H,若∠ABC=20°,则∠CEG-∠CDH=________度.
【答案】110°
【解析】
延长BC交FG于点M,根据AB∥FG,∠ABC=20°得∠CMD=20°,设∠CDH=x°,则∠DCH=∠BCE=90°- x°,则∠CEM==70°- x°,从而表示出∠CEG=110°+ x°,即可求出∠CEG-∠CDH的度数.
解:如图,延长BC交FG于点M,
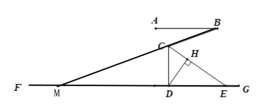
∵AB∥FG,∠ABC=20°,
∴∠CMD=20°,
设∠CDH=x°,
∵DH⊥CE,
∴∠DCH=90°- x°,
又∵CE平分∠BCD,
∴∠BCE=90°- x°,
∴∠CEM=∠BCE-∠CMD=90°- x°-20°=70°- x°,
∴∠CEG=180°-∠CEM=180°-(70°- x°)=110°+ x°,
∴∠CEG-∠CDH=110°+ x°- x°=110°,
故答案为: 110°.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:
【题目】如图,有两种形状不同的直角三角形纸片各两块,其中一种纸片的两条直角边长分别为1和2,另一种纸片的两条直角边长都为2.

图1、图2、图3是三张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1. 请用三种方法将图中所给四块直角三角形纸片全部用上,互不重叠且不留空隙,三种方法所拼得的平行四边形(非矩形)的周长互不相等,并把你所拼得的图形按实际大小画在图1、图2、图3的方格纸上.
要求:(1)所画图形各顶点必须与方格纸中的小正方形顶点重合;



(2)画图时,要保留四块直角三角形纸片的拼接痕迹.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校的复印任务原来由甲复印社承包,其收费y(元)与复印页数x(页)的关系如下表:
x(页) | 100 | 200 | 400 | 1000 | … |
y(元) | 40 | 80 | 160 | 400 | … |
(1)根据表格信息写出y与x之间的关系式;
(2)现在乙复印社表示:若学校每月先付200元的承包费,则可按每页0.15元收费.乙复印社每月收费y(元)与复印页数x(页)之间的关系式为_______________;
(3)若学校每月复印页数在1200页左右,应选择哪个复印社?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:a是最小的正整数,且a,b,c满足|a+b|+(c﹣5)2=0,请回答问题.
(1)请直接写出a、b、c的值;
(2)a、b、c所对应的点分别为A、B、C,点P为一动点,其对应的数为x,点P在A、B之间运动时,请化简式子:|x+1|﹣|x﹣1|﹣2|x+4|(请写出化简过程)
![]()
(3)在(1)(2)的条件下,点A、B、C开始在数轴上运动,若点B以每秒n(n>0)个单位长度的速度向左运动,同时,点A和点C分别以每秒2n个单位长度和5n个单位长度的速度向右运动,假设经过t秒钟过后,若点A与点C之间的距离表示为AC,点A与点B之间的距离表示为AB,请问:AC﹣AB的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图MN∥PQ,点A、B分别在MN、PQ上,∠ABP=80°,射线BC平分∠ABP,且∠CAM=25°,则∠ACB的度数为__________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
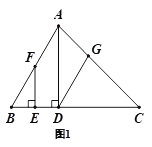
【题目】已知,在三角形ABC中,AD⊥BC于D,F是AB上一点,FE⊥BC于E,∠ADG=∠BFE
(1)如图1,求证:DG∥AB
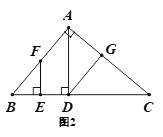
(2)如图2,若∠BAC=90°,请直接写出图中与∠CAD互余的角,不需要证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在双曲线y= ![]() 上,点B在双曲线y=
上,点B在双曲线y= ![]() (k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为( )
(k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为( ) 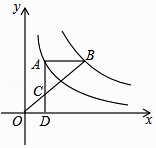
A.6
B.9
C.10
D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,点D是AC上的一点,在BC上取一点E,使BE=CD,连接AE交BD于点P,在BD的延长线上取一点Q,使AP=PQ,连接AQ、CQ,点G为PQ的中点,DG=PE,若CQ=![]() ,则BQ=________________.
,则BQ=________________.
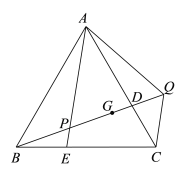
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=120°,BC=6cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为( ) 
A.4cm
B.3cm
C.2cm
D.1cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com