
【题目】如图,已知数轴上点A表示的数为8,B是数轴上位于点A左侧一点,且AB=20,动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t秒.
![]()
(1)数轴上点B表示的数是 ,点P表示的数是 ;(用含t的代数式表示)
(2)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向右匀速运动,若点P、Q同时出发,问多少秒时,P、Q之间的距离恰好等于2;
(3)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发,直接写出多少秒时,P、Q之间的距离恰好等于2.
【答案】(1)﹣12;8﹣5t;(2)若点P、Q同时出发,2.25或2.75秒时P、Q之间的距离恰好等于2;(3)若点P、Q同时出发,9或11秒时P、Q之间的距离恰好又等于2.
【解析】
(1)根据A点表示的数和AB=20即可求出点B表示的数;同样可以利用点A和A,P之间的距离求P点表示的数;
(2)分两种情况:两点相遇之前和相遇之后,相遇之前有3t+2+5t=20,相遇之后有3t﹣2+5t=20,分别解方程即可
(3)同样分两种情况:点P追上点Q之前和点P追上点Q之后,追上之前有5x﹣3x=20﹣2,追上之后有5x﹣3x=20+2,分别解方程即可.
(1)∵数轴上点A表示的数为8,AB=20,AP=5t,
∴数轴上点B表示的数为8﹣20=﹣12;点P表示的数为8﹣5t;
故答案是:﹣12;8﹣5t;
(2)若点P、Q同时出发,设t秒时P、Q之间的距离恰好等于2.分两种情况:
①点P、Q相遇之前,
由题意得3t+2+5t=20,解得t=2.25;
②点P、Q相遇之后,
由题意得3t﹣2+5t=20,解得t=2.75.
答:若点P、Q同时出发,2.25或2.75秒时P、Q之间的距离恰好等于2;
(3)设点P运动x秒时,P、Q之间的距离恰好等于2.分两种情况:
①点P追上点Q之前,
则5x﹣3x=20﹣2,
解得:x=9;
②点P追上点Q之后,
则5x﹣3x=20+2
解得:x=11.
答:若点P、Q同时出发,9或11秒时P、Q之间的距离恰好又等于2.


科目:初中数学 来源: 题型:
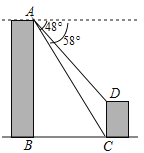
【题目】如图,甲、乙两座建筑物的水平距离BC为78m,从甲的顶部A处测得乙的顶部D处的俯角为48°,测得底部C处的俯角为58°,求乙建筑物的高度CD.(结果取整数,参考数据:tan58°≈1.60,tan48°≈1.11).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知多项式![]() 是关于
是关于![]() 的二次二项式.
的二次二项式.
(1)请填空:![]() ______;
______;![]() ______;
______;![]() ______;
______;
(2)如图,若![]() ,
,![]() 两点在线段
两点在线段![]() 上,且
上,且![]() ,
,![]() ,
,![]() 两点分别是线段
两点分别是线段![]() ,
,![]() 的中点,且
的中点,且![]() ,求线段
,求线段![]() 的长;
的长;
![]()
(3)如图,若![]() ,
,![]() ,
,![]() 分别是数轴上
分别是数轴上![]() ,
,![]() ,
,![]() 三点表示的数,
三点表示的数,![]() 点与
点与![]() 点到原点的距离相等,且位于原点两侧,现有两动点
点到原点的距离相等,且位于原点两侧,现有两动点![]() 和
和![]() 在数轴上同时开始运动,其中点
在数轴上同时开始运动,其中点![]() 先以2个单位每秒的速度从
先以2个单位每秒的速度从![]() 点运动到
点运动到![]() 点,再以5个单位每秒的速度运动到
点,再以5个单位每秒的速度运动到![]() 点,最后以8个单位每秒的速度返回到
点,最后以8个单位每秒的速度返回到![]() 点停止运动;而动点
点停止运动;而动点![]() 先以2个单位每秒的速度从
先以2个单位每秒的速度从![]() 点运动到
点运动到![]() 点,再以12个单位每秒的速度返回到
点,再以12个单位每秒的速度返回到![]() 点停止运动.在此运动过程中,
点停止运动.在此运动过程中,![]() ,
,![]() 两点到
两点到![]() 点的距离是否会相等?若相等,请直接写出此时点
点的距离是否会相等?若相等,请直接写出此时点![]() 在数轴上表示的数;若不相等,请说明理由.
在数轴上表示的数;若不相等,请说明理由.
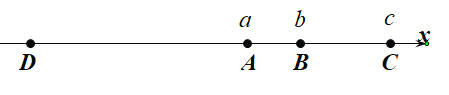
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,李老师和同学们做一个游戏:他在三张硬纸片上分别写出一个代数式,背面分别标上序号①、②、③,摆成如图所示的一个等式,然后翻开纸片②是4x2+5x+6,翻开纸片③是3x2﹣x﹣2.
![]()
解答下列问题
(1)求纸片①上的代数式;
(2)若x是方程2x=﹣x﹣9的解,求纸片①上代数式的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列说法:其中正确的个数是()
(1)有一个角为60°的等腰三角形是等边三角形;
(2)三角之比为3:4:5的三角形为直角三角形;
(3)等腰三角形的两条边长为2,4,则等腰三角形的周长为10;
(4)一边上的中线等于这边长的一半的三角形是等边三角形;
A.2个B.3个C.4个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
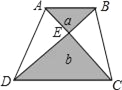
【题目】如图,梯形ABCD中,AB∥CD,两条对角线交于点E.已知△ABE的面积是a,△CDE的面积是b,则梯形ABCD的面积是( )
A. a2+b2 B. ![]() (a+b) C.
(a+b) C. ![]() D. (a+b)2
D. (a+b)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,在四边形ABCD中,AD∥BC,AB⊥BC,对角线AC⊥CD,点E在边BC上,且∠AEB=45°,CD=10.

(1)求AB的长;
(2)求EC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com