
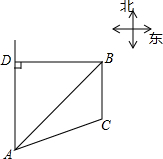
 已知B港口位于A观测点的东北方向,且其到A观测点正北方向的距离BD的长为16千米,一艘货轮从B港口以48千米/时的速度沿如图所示的BC方向航行,15分后到达C处,现测得C处位于A观测点北偏东75°方向,求此时货轮与A观测点之间的距离AC的长(精确大0.1千米)
已知B港口位于A观测点的东北方向,且其到A观测点正北方向的距离BD的长为16千米,一艘货轮从B港口以48千米/时的速度沿如图所示的BC方向航行,15分后到达C处,现测得C处位于A观测点北偏东75°方向,求此时货轮与A观测点之间的距离AC的长(精确大0.1千米)分析 根据在Rt△ADB中,sin∠DAB=$\frac{DB}{AB}$,得出AB的长,进而得出tan∠BAH=$\frac{BH}{AH}$,求出BH的长,即可得出AH以及CH的长,进而得出答案.
解答 解:BC=48×$\frac{15}{60}$=12,
在Rt△ADB中,sin∠DAB=$\frac{DB}{AB}=\frac{\sqrt{2}}{2}$,
∴AB=$\frac{16}{\frac{\sqrt{2}}{2}}$=16$\sqrt{2}$,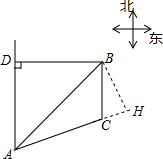 如图,过点B作BH⊥AC,交AC的延长线于H,
如图,过点B作BH⊥AC,交AC的延长线于H,
在Rt△AHB中,∠BAH=∠DAC-∠DAB=75°-45°=30°,
tan∠BAH=$\frac{BH}{AH}$=$\frac{\sqrt{3}}{3}$,
∴AH=$\sqrt{3}$BH,
BH2+AH2=AB2,BH2+($\sqrt{3}$BH)2=(16$\sqrt{2}$)2,∴BH=8$\sqrt{2}$,∴AH=8$\sqrt{6}$,
在Rt△BCH中,BH2+CH2=BC2,∴CH=4,
∴AC=AH-CH=8$\sqrt{6}$-4≈15.7km,
答:此时货轮与A观测点之间的距离AC约为15.7km.
点评 此题主要考查了解直角三角形中方向角问题,根据已知构造直角三角形得出BH的长是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
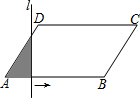 如图,?ABCD中,AD=6,∠A=60°,AB=10,直线l⊥AB,且从点A开始向右匀速平行移动,每秒运动1个单位长度,设直线l扫过?ABCD的面积(阴影部分)为y,移动的时间为x秒,则当3≤x<10时,y与x的函数关系式是y=$\frac{3\sqrt{3}}{2}$x2-$\frac{9\sqrt{3}}{2}$x.
如图,?ABCD中,AD=6,∠A=60°,AB=10,直线l⊥AB,且从点A开始向右匀速平行移动,每秒运动1个单位长度,设直线l扫过?ABCD的面积(阴影部分)为y,移动的时间为x秒,则当3≤x<10时,y与x的函数关系式是y=$\frac{3\sqrt{3}}{2}$x2-$\frac{9\sqrt{3}}{2}$x.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 工种 | 人数 | 每人每月工资/元 |
| 电工 | 6 | 7000 |
| 木工 | 4 | 6000 |
| 瓦工 | 6 | 5000 |
| A. | 变大 | B. | 不变 | C. | 变小 | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
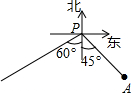 如图,小岛A在港口P的南偏东45°方向、距离港口81海里处.甲船从A出发,沿AP方向以9海里/h的速度驶向港口;乙船从港口P出发,沿南偏西60°方向,以18海里/h的速度驶离港口.现两船同时出发,当甲船在乙船的正东方向时,行驶的时间为9($\sqrt{2}$-1)h.(结果保留根号)
如图,小岛A在港口P的南偏东45°方向、距离港口81海里处.甲船从A出发,沿AP方向以9海里/h的速度驶向港口;乙船从港口P出发,沿南偏西60°方向,以18海里/h的速度驶离港口.现两船同时出发,当甲船在乙船的正东方向时,行驶的时间为9($\sqrt{2}$-1)h.(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com