
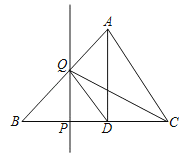
【题目】如图,△ABC中,AD⊥BC,垂足为D,AD=BD=3,CD=2,点P从点B出发沿线段BC的方向移动到点C停止,过点P作PQ⊥BC,交折线BA﹣AC于点Q,连接DQ、CQ,若△ADQ与△CDQ的面积相等,则线段BP的长度是_____.
【答案】![]() 或4.
或4.
【解析】
分两种情况讨论:①点Q在AB边上时,设BP=x,用x表示出S△DCQ和 S△AQD,即可求解;②当Q在AC上时,则△AD Q与△CD Q的面积相等可得AQ=CQ,据此可求解.
解:分两种情况讨论:
①点Q在AB边上时,
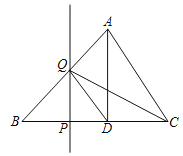
∵AD⊥BC,AD=BD=3,CD=2,
∴S△ABD=![]() BDAD=
BDAD=![]() ×3×3=
×3×3=![]() ,∠B=45°,
,∠B=45°,
∵PQ⊥BC,
∴BP=PQ,
设BP=x,则PQ=x,PD= 3-x,
∵CD=2,
∴S△DCQ=![]() ×2x=x,
×2x=x,
S△AQD=![]() ×3×(3-x)
×3×(3-x)
=![]() ﹣
﹣![]() x
x
∵△ADQ与△CDQ的面积相等,
∴x=![]() ﹣
﹣![]() x,
x,
解得x=![]() ;
;
②如图,当Q在AC上时,记为Q',过点Q'作Q'P'⊥BC,
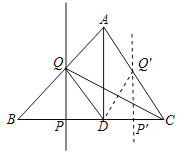
∵AD⊥BC,
∴Q'P'∥AD,
∵△AD Q'与△CD Q'的面积相等,
∴AQ'=CQ',
∴DQ'是Rt△ADC斜边上的中线,
∴DQ'= CQ',
∴P' Q'是CD的垂直平分线,
∴DP'=CP'=![]() CD=1,
CD=1,
∵AD=BD=3,
∴BP'=BD+DP'=4,
综上所述,线段BP的长度是![]() 或4.
或4.
故答案为:![]() 或4.
或4.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() ,与x轴交于点C,
,与x轴交于点C,![]() 点C在点D的左侧
点C在点D的左侧![]() ,与y轴交于点A.
,与y轴交于点A.
![]() 求抛物线顶点M的坐标;
求抛物线顶点M的坐标;
![]() 若点A的坐标为
若点A的坐标为![]() ,
,![]() 轴,交抛物线于点B,求点B的坐标;
轴,交抛物线于点B,求点B的坐标;
![]() 在
在![]() 的条件下,将抛物线在B,C两点之间的部分沿y轴翻折,翻折后的图象记为G,若直线
的条件下,将抛物线在B,C两点之间的部分沿y轴翻折,翻折后的图象记为G,若直线![]() 与图象G有一个交点,结合函数的图象,求m的取值范围.
与图象G有一个交点,结合函数的图象,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于点A和B(3,0),与y轴交于点C(0,3).
(1)求抛物线的解析式;
(2)若点M是抛物线上在x轴下方的动点,过M作MN∥y轴交直线BC于点N,求线段MN的最大值;
(3)E是抛物线对称轴上一点,F是抛物线上一点,是否存在以A,B,E,F为顶点的四边形是平行四边形?若存在,请直接写出点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC的底边BC=20,面积为120,点F在边BC上,且BF=3FC,EG是腰AC的垂直平分线,若点D在EG上运动,则△CDF周长的最小值为__.
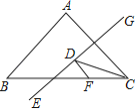
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E、G分别是边AD、BC的中点,AF=![]() AB.
AB.
(1)求证:EF⊥AG;
(2)若点F、G分别在射线AB、BC上同时向右、向上运动,点G运动速度是点F运动速度的2倍,EF⊥AG是否成立(只写结果,不需说明理由)?
(3)正方形ABCD的边长为4,P是正方形ABCD内一点,当![]() ,求△PAB周长的最小值.
,求△PAB周长的最小值.
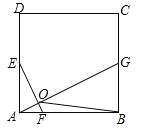
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以点P为端点竖直向下的一条射线PN,以它为对称轴向左右对称摆动形成了射线PN1,PN2,我们规定:∠N1PN2为点P的“摇摆角”,射线PN摇摆扫过的区域叫作点P的“摇摆区域”(含PN1,PN2).
在平面直角坐标系xOy中,点P(2,3).
(1)当点P的摇摆角为60°时,请判断O(0,0)、A(1,2)、B(2,1)、C(2+![]() ,0)属于点P的摇摆区域内的点是 (填写字母即可);
,0)属于点P的摇摆区域内的点是 (填写字母即可);
(2)如果过点D(1,0),点E(5,0)的线段完全在点P的摇摆区域内,那么点P的摇摆角至少为 °;
(3)⊙W的圆心坐标为(a,0),半径为1,如果⊙W上的所有点都在点P的摇摆角为60°时的摇摆区域内,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣![]() x2+3x﹣
x2+3x﹣![]()
(1)用配方法求出函数图象的顶点坐标和对称轴方程;
(2)用描点法在如图所示的平面直角坐标系中画出该函数的图象;
(3)根据图象,直接写出y的值小于0时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:sin(﹣x)=﹣sinx,cos(﹣x)=cosx,sin(x+y)=sinxcosy+cosxsiny.
据此判断下列等式成立的是 (写出所有正确的序号)
①cos(﹣60°)=﹣![]() ;
;
②sin75°=![]() ;
;
③sin2x=2sinxcosx;
④sin(x﹣y)=sinxcosy﹣cosxsiny.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义![]() 为一次函数y=px+q的特征数.
为一次函数y=px+q的特征数.
(1)若特征数是![]() 的一次函数为正比例函数,求m的值;
的一次函数为正比例函数,求m的值;
(2)已知抛物线y=(x+n)(x-2)与x轴交于点A、B,其中n>0,点A在点B的左侧,与y轴交于点C,且△OAC的面积为4,O为原点,求图象过A、C两点的一次函数的特征数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com