
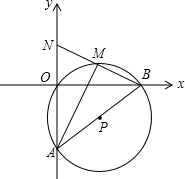
 如图,在平面直角坐标系中,O(0,0),A(0,-6),B(8,0)三点在⊙P上.
如图,在平面直角坐标系中,O(0,0),A(0,-6),B(8,0)三点在⊙P上.分析 (1)先利用勾股定理计算出AB=10,再利用圆周角定理的推理可判断AB为⊙P的直径,则得到⊙P的半径是5,然后利用线段的中点坐标公式得到P点坐标;
(2)根据圆周角定理由$\widehat{OM}$=$\widehat{BM}$,∠OAM=∠MAB,于是可判断AM为∠OAB的平分线;
(3)连接PM交OB于点Q,如图,先利用垂径定理的推论得到PM⊥OB,BQ=OQ=$\frac{1}{2}$OB=4,再利用勾股定理计算出PQ=3,则MQ=2,于是可写出M点坐标,接着证明MQ为△BON的中位线得到ON=2MQ=4,然后写出N点的坐标.
解答 解:(1)∵O(0,0),A(0,-6),B(8,0),
∴OA=6,OB=8,
∴AB=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵∠AOB=90°,
∴AB为⊙P的直径,
∴⊙P的半径是5
∵点P为AB的中点,
∴P(4,-3);
(2)∵M点是劣弧OB的中点,
∴$\widehat{OM}$=$\widehat{BM}$,
∴∠OAM=∠MAB,
∴AM为∠OAB的平分线;
(3)连接PM交OB于点Q,如图,
∵$\widehat{OM}$=$\widehat{BM}$,
∴PM⊥OB,BQ=OQ=$\frac{1}{2}$OB=4,
在Rt△PBQ中,PQ=$\sqrt{P{B}^{2}-B{Q}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3,
∴MQ=2,
∴M点的坐标为(4,2);
∵MQ∥ON,
而OQ=BQ,
∴MQ为△BON的中位线,
∴ON=2MQ=4,
∴N点的坐标为(0,4).
点评 本题考查了圆的综合题:熟练掌握垂径定理和圆周角定理;理解坐标与图形的性质,记住线段的中点坐标公式,会利用勾股定理计算线段的长.此类题目通常解由半径、弦心距和弦的一半所组成的直角三角形.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:选择题
| A. | x>-1 | B. | x<$\frac{1}{2}$ | C. | -1<x<$\frac{1}{2}$ | D. | x>$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
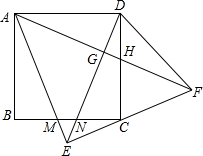 如图,正方形ABCD中,以AD为底边作等腰△ADE,将△ADE沿DE折叠,点A落到点F处,连接EF刚好经过点C,再连接AF,分别交DE于G,交CD于H.在下列结论中:
如图,正方形ABCD中,以AD为底边作等腰△ADE,将△ADE沿DE折叠,点A落到点F处,连接EF刚好经过点C,再连接AF,分别交DE于G,交CD于H.在下列结论中:| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
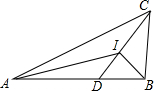 如图,在△ABC中,AB=6,BC=3,CA=7,I为△ABC的内心,连接CI并延长交AB于点D.记△CAI的面积为m,△DAI的面积为n,则$\frac{m}{n}$=( )
如图,在△ABC中,AB=6,BC=3,CA=7,I为△ABC的内心,连接CI并延长交AB于点D.记△CAI的面积为m,△DAI的面积为n,则$\frac{m}{n}$=( )| A. | $\frac{3}{2}$ | B. | $\frac{4}{3}$ | C. | $\frac{5}{3}$ | D. | $\frac{7}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
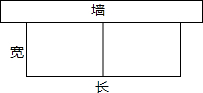 有长为30m的篱笆,一面利用墙(墙的可用长度不能超过16m)围成一块矩形花圃,如图所示:
有长为30m的篱笆,一面利用墙(墙的可用长度不能超过16m)围成一块矩形花圃,如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com