
如图:抛物线y=-x2+bx+c交x轴于A、B,直线y=x+2过点A,交y轴于C,交抛物线于D,且D的纵坐标为5.
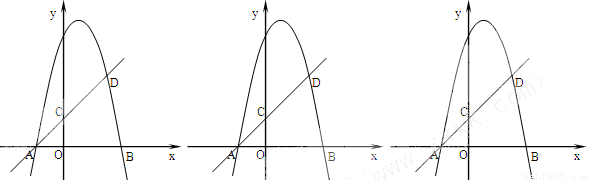
(1)求抛物线解析式;
(2)点P为抛物线在第一象限的图象上一点,直线PC交x轴于点E,若PC=3CE,求点P的坐标;
(3)在(2)的条件下,点Q为x轴上一点,把△PCQ沿CQ翻折,点P刚好落在x轴上点G处,求Q点的坐标.
(1)y=-x2+2x+8;(2)P(2,8);(3)Q(-4,0)或Q(2,0).
【解析】
试题分析:(1)将已知点的坐标代入二次函数的一般形式利用待定系数法确定二次函数的解析式即可;
(2)设P(m,-m2+2m+8),作PH⊥x轴,交x轴于点H,从而得到△EOC∽△EHP,利用相似三角形对应边的比相等得到PH=4OC,从而列出方程-m2+2m+8=4×2,求得m的值即可确定点的坐标;
(3)作PK⊥y轴,从而得到PK=2,KC=8-2=6,然后由翻折得△CQG≌△CQP,从而得到QG=QP,CG=CP=2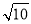 ,然后在Rt△OCG中求得GO的长即可求得点G的坐标.
,然后在Rt△OCG中求得GO的长即可求得点G的坐标.
试题解析:(1)∵y=x+2,
∴A(-2,0),
∵D的纵坐标为5,
∴5=x+2,
解得:x=3
∴D(3,5),
又∵A(-2,0)D(3,5)在抛物线y=-x2+bx+c上,
∴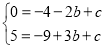
解得
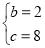
∴抛物线的解析式为y=-x2+2x+8;
(2)设P(m,-m2+2m+8),
作PH⊥x轴,交x轴于点H,
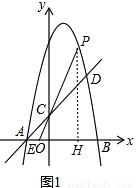
∴CO∥PH,
∴△EOC∽△EHP,
∴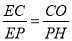 ,
,
∵PC=3CE,
∴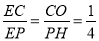 ,
,
∴PH=4OC,
∴-m2+2m+8=4×2,
解得 m=2,或m=0(舍去),
∴P(2,8);
(3)作PK⊥y轴,
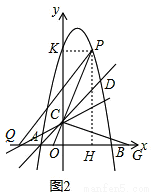
∴PK=2,KC=8-2=6,
在Rt△CPK中,CP=2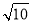 ,
,
由翻折得△CQG≌△CQP,
∴QG=QP,CG=CP=2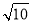 ,
,
在Rt△OCG中,
∵CP=2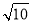 ,OC=2,
,OC=2,
∴GO=6,
∴G(6,0)或G(-6,0),
过P作PH⊥x轴,则H(2,0),且PH=8,

设Q(n,0)
则QP2=PH2+QH2=82+(n-2)2,
GQ=|xQ-xG|=|n-(±6)|
因为QG=QP,
82+(n-2)2=[n-(±6)]2,
解得n=-4,或n=2,
∴Q(-4,0)或Q(2,0).
考点:二次函数综合题.


科目:初中数学 来源:2014-2015学年江苏省盐城市盐都区九年级上学期期末考试数学试卷(解析版) 题型:填空题
请写出一个开口向上,与y轴交点的纵坐标为2的抛物线的函数表达式 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省苏州市九年级上学期期末考试数学试卷(解析版) 题型:选择题
方程x2=2x的解是( )
A.x=2 B.x1=2, x2=0 C.x1=-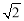 ,x2=0 D.x=0
,x2=0 D.x=0
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖南省耒阳市九年级上学期期末考试数学试卷(解析版) 题型:选择题
如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( )

A.2 B.2
B.2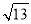 C.2
C.2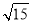 D.8
D.8
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖南省耒阳市九年级上学期期末考试数学试卷(解析版) 题型:选择题
⊙A半径为5,圆心A的坐标为(1,0),点P的坐标为(-2,4),则点P与⊙A的位置关系是( )
A.点P在⊙A上 B.点P在⊙A内
C.点P在⊙A外 D.点P在⊙A上或外
查看答案和解析>>
科目:初中数学 来源:2014-2015学年黑龙江省五常市九年级上学期12月阶段性测试数学试卷(解析版) 题型:解答题
在△ABC中,AD是BC边上的高,∠B=30°,∠C=45°,CD=2.求BC的长.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年河南省郑州市九年级第一次质量预测数学试卷(解析版) 题型:解答题
(10分)如图①,正方形AEFG的边长为1,正方形ABCD的边长为3,且点F在AD上.
(1)求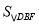 ;
;
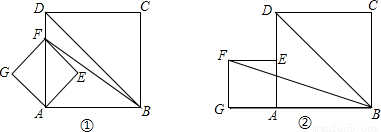
(2)把正方形AEFG绕点A按逆时针方向旋转45°得图②,求图②中的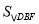 ;
;
(3)把正方形AEFG绕点A旋转一周,在旋转的过程中,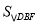 存在最大值与最小值,请直接写出最大值 ,最小值 .
存在最大值与最小值,请直接写出最大值 ,最小值 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河北省石家庄市九年级上学期第二次月考数学试卷(解析版) 题型:选择题
某商品经过两次降价,由单价100元调至81元,则平均每次降价的百分率是( )
A.8.5﹪ B.9﹪ C.9.5 ﹪ D.10﹪
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com