
ЁОЬтФПЁПЮЊСЫМгЧПЙЋУёЕФНкЫЎвтЪЖЃЌКЯРэРћгУЫЎзЪдДЃЌФГГЧЪаЙцЖЈгУЫЎЪеЗбБъзМШчЯТЃКУПЛЇУПдТгУЫЎСПВЛГЌЙ§6Уз3ЪБЃЌЫЎЗбАДaдЊ/Уз3ЪеЗбЃЛУПЛЇУПдТгУЫЎСПГЌЙ§6Уз3ЪБЃЌВЛГЌЙ§ЕФВПЗжУПСЂЗНУзШдАДaдЊЪеЗбЃЌГЌЙ§ЕФВПЗжАДcдЊ/Уз3ЪеЗбЃЌИУЪаФГгУЛЇНёФъ3ЁЂ4дТЗнЕФгУЫЎСПКЭЫЎЗбШчЯТБэЫљЪОЃК
дТЗн | гУЫЎСП(m3) | ЪеЗб(дЊ) |
3 | 5 | 7.5 |
4 | 9 | 27 |
(1)ЧѓaЁЂcЕФжЕЃЌВЂаДГіУПдТгУЫЎСПВЛГЌЙ§6Уз3КЭГЌЙ§6Уз3ЪБЃЌЫЎЗбгыгУЫЎСПжЎМфЕФЙиЯЕЪНЃЛ
(2)вбжЊФГЛЇ5дТЗнЕФгУЫЎСПЮЊ8Уз3ЃЌЧѓИУгУЛЇ5дТЗнЕФЫЎЗбЃЎ
ЁОД№АИЁП(1)![]() ЃЛ0ЁмxЁм6ЪБЃЌy=1.5xЃЛ xЃО6ЪБЃЌy=6x-27ЃЛ(2)ИУЛЇ5дТЗнЫЎЗбЪЧ21дЊЃЎ
ЃЛ0ЁмxЁм6ЪБЃЌy=1.5xЃЛ xЃО6ЪБЃЌy=6x-27ЃЛ(2)ИУЛЇ5дТЗнЫЎЗбЪЧ21дЊЃЎ
ЁОНтЮіЁП
(1)ИљОн3ЁЂ4СНИідТЕФгУЫЎСПКЭЯргІЫЎЗбСаЗНГЬзщЧѓНтПЩЕУaЁЂcЕФжЕЃЛЕБ0ЁмxЁм6ЪБЃЌЫЎЗб=гУЫЎСПЁСДЫЪБЕЅМлЃЛЕБxЃО6ЪБЃЌЫЎЗб=ЧА6СЂЗНЫЎЗб+ГЌГіВПЗжЫЎЗбЃЌОнДЫСаЪНМДПЩЃЛ (2)x=8ДњШыxЃО6ЪБyгыxЕФКЏЪ§ЙиЯЕЪНЧѓНтМДПЩЃЎ
НтЃК(1)ИљОнЬтвтЃЌЕУЃК ЃЌ
ЃЌ
НтЕУЃК![]() ЃЛ
ЃЛ
ЕБ0ЁмxЁм6ЪБЃЌy=1.5xЃЛ
ЕБxЃО6ЪБЃЌy=1.5ЁС6+6(x-6)=6x-27ЃЛ
(2)ЕБx=8ЪБЃЌy=6x-27=6ЁС8-27=21ЃЎ
Д№ЃКШєФГЛЇ5дТЗнЕФгУЫЎСПЮЊ8Уз3ЃЌИУЛЇ5дТЗнЫЎЗбЪЧ21дЊЃЎ


 ЪжРЪжШЋгХСЗПМОэЯЕСаД№АИ
ЪжРЪжШЋгХСЗПМОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
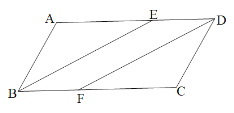
ЁОЬтФПЁПШчЭМЃЌABCDжаЃЌ![]() ЕФНЧЦНЗжЯп
ЕФНЧЦНЗжЯп![]() НЛADгкЕуEЃЌ
НЛADгкЕуEЃЌ![]() ЕФНЧЦНЗжЯп
ЕФНЧЦНЗжЯп![]() НЛ
НЛ![]() ЁЁгкЕу
ЁЁгкЕу![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() =50Ёу.
=50Ёу.
ЃЈ1ЃЉЧѓ![]() ЕФЖШЪ§ЃЛ
ЕФЖШЪ§ЃЛ
ЃЈ2ЃЉЧѓABCDЕФжмГЄ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПДгШ§НЧаЮЃЈВЛЪЧЕШбќШ§НЧаЮЃЉвЛИіЖЅЕув§ГівЛЬѕЩфЯпгкЖдБпЯрНЛЃЌЖЅЕугыНЛЕужЎМфЕФЯпЖЮАбетИіШ§НЧаЮЗжИюГЩСНИіаЁШ§НЧаЮЃЌШчЙћЗжЕУЕФСНИіаЁШ§НЧаЮжавЛИіЮЊЕШбќШ§НЧаЮЃЌСэвЛИігыдШ§НЧаЮЯрЫЦЃЌЮвУЧАбетЬѕЯпЖЮНазіетИіШ§НЧаЮЕФЭъУРЗжИюЯпЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌдкЁїABCжаЃЌCDЮЊНЧЦНЗжЯпЃЌЁЯA=40ЁуЃЌЁЯB=60ЁуЃЌЧѓжЄЃКCDЮЊЁїABCЕФЭъУРЗжИюЯпЃЎ
ЃЈ2ЃЉдкЁїABCжаЃЌЁЯA=48ЁуЃЌCDЪЧЁїABCЕФЭъУРЗжИюЯпЃЌЧвЁїACDЮЊЕШбќШ§НЧаЮЃЌЧѓЁЯACBЕФЖШЪ§ЃЎ
ЃЈ3ЃЉШчЭМ2ЃЌЁїABCжаЃЌAC=2ЃЌBC=![]() ЃЌCDЪЧЁїABCЕФЭъУРЗжИюЯпЃЌЧвЁїACDЪЧвдCDЮЊЕзБпЕФЕШбќШ§НЧаЮЃЌЧѓЭъУРЗжИюЯпCDЕФГЄЃЎ
ЃЌCDЪЧЁїABCЕФЭъУРЗжИюЯпЃЌЧвЁїACDЪЧвдCDЮЊЕзБпЕФЕШбќШ§НЧаЮЃЌЧѓЭъУРЗжИюЯпCDЕФГЄЃЎ
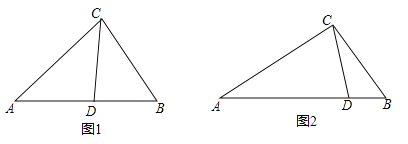
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ1ЃЉШчЭМЃЈ1ЃЉЃЌвбжЊЃКдкЁїABCжаЃЌЁЯBACЃН90ЁуЃЌAB=ACЃЌжБЯпmОЙ§ЕуAЃЌBDЁЭжБЯпm, CEЁЭжБЯпm,ДЙзуЗжБ№ЮЊЕуDЁЂE.жЄУї:DE=BD+CE.
ЃЈ2ЃЉ ШчЭМЃЈ2ЃЉЃЌНЋЃЈ1ЃЉжаЕФЬѕМўИФЮЊЃКдкЁїABCжаЃЌAB=ACЃЌDЁЂAЁЂEШ§ЕуЖМдкжБЯпmЩЯ,ВЂЧвгаЁЯBDA=ЁЯAEC=ЁЯBAC=![]() ,Цфжа
,Цфжа![]() ЮЊШЮвтШёНЧЛђЖлНЧ.ЧыЮЪНсТлDE=BD+CEЪЧЗёГЩСЂ?ШчГЩСЂ,ЧыФуИјГіжЄУї;ШєВЛГЩСЂ,ЧыЫЕУїРэгЩ.
ЮЊШЮвтШёНЧЛђЖлНЧ.ЧыЮЪНсТлDE=BD+CEЪЧЗёГЩСЂ?ШчГЩСЂ,ЧыФуИјГіжЄУї;ШєВЛГЩСЂ,ЧыЫЕУїРэгЩ.
ЃЈ3ЃЉЭиеЙгыгІгУЃКШчЭМЃЈ3ЃЉЃЌDЁЂEЪЧDЁЂAЁЂEШ§ЕуЫљдкжБЯпmЩЯЕФСНЖЏЕуЃЈDЁЂAЁЂEШ§ЕуЛЅВЛжиКЯЃЉ,ЕуFЮЊЁЯBACЦНЗжЯпЩЯЕФвЛЕу,ЧвЁїABFКЭЁїACFОљЮЊЕШБпШ§НЧаЮЃЌСЌНгBDЁЂCE,ШєЁЯBDA=ЁЯAEC=ЁЯBACЃЌЪдХаЖЯЁїDEFЕФаЮзД.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫНтбЇЩњЬхг§ЛюЖЏЕФЧщПіЃЌбЇаЃЩшМЦСЫЁАФузюЯВЛЖЕФЬхг§ЛюЖЏЪЧФФвЛЯюЃЈНіЯовЛЯюЃЉЁБЕФЕїВщЮЪОэЃЎИУаЃЖдбЇЩњНјааЫцЛњГщбљЕїВщЃЌвдЯТЪЧИљОнЕїВщЪ§ОнЕУЕНЕФВЛЭъећЕФЭГМЦЭМЃЎЧыИљОнЭГМЦЭМжааХЯЂНтД№вдЯТЮЪЬтЃК
ЃЈ1ЃЉИУаЃЖдЖрЩйУћбЇЩњНјааСЫГщбљЕїВщЃП
ЃЈ2ЃЉЂйЧыВЙШЋЭМ1ВЂБъЩЯЪ§ОнЃЌ
ЁЁЂкЭМ2жаx=__________% ЃЛ
ЃЈ3ЃЉШєИУаЃЙВгабЇЩњ900ШЫЃЌЧыФуЙРМЦИУаЃзюЯВЛЖЬјЩўЯюФПЕФбЇЩњдМгаЖрЩйШЫЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ,вбжЊЁїABDКЭЁїACDЙигкжБЯпADЖдГЦЃЛдкЩфЯпADЩЯШЁЕуE,СЌНгBE, CE,ШчЭМ:дкЩфЯпADЩЯШЁЕуFСЌНгBF, CF,ШчЭМ,вРДЫЙцТЩЃЌЕкnИіЭМаЮжаШЋЕШШ§НЧаЮЕФЖдЪ§ЪЧЃЈ ЃЉ

A.nB.2n-1C.![]() D.3(n+1)
D.3(n+1)
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌAЕузјБъЮЊЃЈЉ4ЃЌЉ3ЃЉЃЌНЋЯпЖЮOAШЦдЕуOЫГЪБеыа§зЊ90ЁуЕУЕНOAЁфЃЌдђЕуAЁфЕФзјБъЪЧЃЈЁЁЁЁЃЉ

A. ЃЈЉ4ЃЌ3ЃЉ B. ЃЈЉ3ЃЌ4ЃЉ C. ЃЈ3ЃЌЉ4ЃЉ D. ЃЈ4ЃЌЉ3ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЪпВЫОгЊЛЇРЯЭѕЃЌНќСНЬьОгЊЕФЪЧЧрВЫКЭЮїРМЛЈЃЎ
ЃЈ1ЃЉзђЬьЕФЧрВЫКЭЮїРМЛЈЕФНјМлКЭЪлМлШчЯТБэЃЌРЯЭѕгУ600дЊХњЗЂЧрВЫКЭЮїРМЛЈЙВ200НяЃЌРЯЭѕзђЬьЧрВЫКЭЮїРМЛЈИїНјСЫЖрЩйНяЃП
ЧрВЫ | ЮїРМЛЈ | |
НјМлЃЈдЊ/НяЃЉ | 2.6 | 3.4 |
ЪлМлЃЈдЊ/НяЃЉ | 3.6 | 4.6 |
ЃЈ2ЃЉНёЬьвђНјМлВЛБфЃЌРЯЭѕШдгУ600дЊХњЗЂЧрВЫКЭЮїРМЛЈЙВ200НяЃЌЕЋдкдЫЪфжаЧрВЫЫ№ЛЕСЫ10%ЃЌЖјЮїРМЛЈУЛгаЫ№ЛЕШдАДзђЬьЕФЪлМлЯњЪлЃЌвЊЯыЕБЬьЪлЭъКѓЫљзЌЕФЧЎВЛЩйгкзђЬьЫљзЌЕФЧЎЃЌЧыФуАяРЯЭѕМЦЫуЃЌЧрВЫУПНяЪлМлжСЩйЮЊЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ1ЃЉВйзїЗЂЯжЃКШчЭМЂйЃЌаЁУїЛСЫвЛИіЕШбќШ§НЧаЮABCЃЌЦфжаAB=ACЃЌдкЁїABCЕФЭтВрЗжБ№вдABЃЌACЮЊбќзїСЫСНИіЕШбќжБНЧШ§НЧаЮABDЃЌACEЃЌЗжБ№ШЁBDЃЌCEЃЌBCЕФжаЕуMЃЌNЃЌGЃЌСЌНгGMЃЌGNЃЎаЁУїЗЂЯжСЫЃКЯпЖЮGMгыGNЕФЪ§СПЙиЯЕЪЧ__________ЃЛЮЛжУЙиЯЕЪЧ__________ЃЎ
ЃЈ2ЃЉРрБШЫМПМЃК
ШчЭМЂкЃЌаЁУїдкДЫЛљДЁЩЯНјааСЫЩюШыЫМПМЃЎАбЕШбќШ§НЧаЮABCЛЛЮЊвЛАуЕФШёНЧШ§НЧаЮЃЌЦфжаABЃОACЃЌЦфЫќЬѕМўВЛБфЃЌаЁУїЗЂЯжЕФЩЯЪіНсТлЛЙГЩСЂТ№ЃПЧыЫЕУїРэгЩЃЎ
ЃЈ3ЃЉЩюШыбаОПЃК
ШчЭМЂлЃЌаЁУїдкЃЈ2ЃЉЕФЛљДЁЩЯЃЌгжзїСЫНјвЛВНЕФЬНОПЃЎЯђЁїABCЕФФкВрЗжБ№зїЕШбќжБНЧШ§НЧаЮABDЃЌACEЃЌЦфЫќЬѕМўВЛБфЃЌЪдХаЖЯЁїGMNЕФаЮзДЃЌВЂИјгыжЄУїЃЎ

ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com