
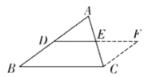
【题目】如图,将![]() 放在每个小正方形的边长为1的网格中,点
放在每个小正方形的边长为1的网格中,点![]() ,点
,点![]() ,点
,点![]() 均落在格点上.
均落在格点上.
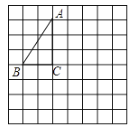
(1)![]() _________.
_________.
(2)请在如图所示的网格中,用无刻度的直尺,画出一个以![]() 为底边的等腰
为底边的等腰![]() ,使该三角形的面积等于
,使该三角形的面积等于![]() 的面积,并简要说明点
的面积,并简要说明点![]() 的位置是如何找到的(不要求证明)__________.
的位置是如何找到的(不要求证明)__________.
科目:初中数学 来源: 题型:
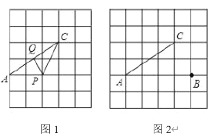
【题目】如图,ABCD中,AB∥x轴,AB=6.点A的坐标为(1,﹣4),点D的坐标为(﹣3,4),点B在第四象限,点G是AD与y轴的交点,点P是CD边上不与点C,D重合的一个动点,过点P作y轴的平行线PM,过点G作x轴的平行线GM,它们相交于点M,将△PGM沿直线PG翻折,当点M的对应点落在坐标轴上时,点P的坐标为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
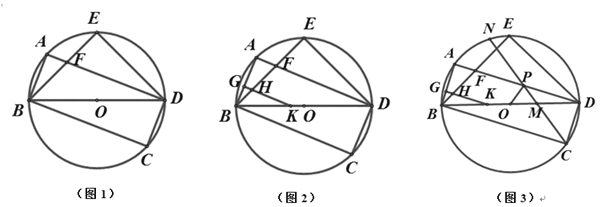
【题目】已知:矩形ABCD内接于⊙O,连接 BD,点E在⊙O上,连接 BE交 AD于点F,∠BDC+45°=∠BFD,连接ED.
(1)如图 1,求证:∠EBD=∠EDB;
(2)如图2,点G是 AB上一点,过点G作 AB的垂线分别交BE和 BD于点H和点K,若HK=BG+AF,求证:AB=KG;
(3)如图 3,在(2)的条件下,⊙O上有一点N,连接 CN分别交BD和 AD于![]() 点 M和点 P,连接 OP,∠APO=∠CPO,若 MD=8,MC= 3,求线段 GB的长.
点 M和点 P,连接 OP,∠APO=∠CPO,若 MD=8,MC= 3,求线段 GB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有3张纸牌,分別是红桃3、红桃4和黑桃5(简称红3,红4,黑5).把牌洗匀后甲先抽取一张,记下花色和数字后将牌放回,洗匀后乙再抽取一张.
(1)两次抽得纸牌均为红桃的概率;(请用“画树状图”或“列表”等方法写出分析过程)
(2)甲、乙两人做游戏,现有两种方案.A方案:若两次抽得花色相同则甲胜,否则乙胜.B方案:若两次抽得纸牌的数字和为奇数则甲胜,否则乙胜.请问甲选择哪种方案胜率更高?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在每个小正方形的边长为1的网格中,点![]() ,
,![]() ,
,![]() 均在格点上,点
均在格点上,点![]() ,
,![]() 分别为线段
分别为线段![]() ,
,![]() 上的动点.
上的动点.
(I)如图(1),当点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 中点时,
中点时,![]() 的值为__________;
的值为__________;
(Ⅱ)当![]() 取得最小值时,在如图(2)所示的网格中,用无刻度的真尺,画出线段
取得最小值时,在如图(2)所示的网格中,用无刻度的真尺,画出线段![]() ,
,![]() ,简要说明点
,简要说明点![]() 和点
和点![]() 的位置是如何找到的(不要求证明)__________.
的位置是如何找到的(不要求证明)__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中考体育测试前,某区教育局为了了解选报引体向上的初三男生的成绩情况,随机抽测了本区部分选报引体向上项目的初三男生的成绩,并将测试得到的成绩绘成了下面两幅不完整的统计图:
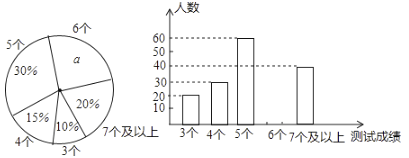
请你根据相关信息,解答下列问题:
(1)写出扇形图中![]() ___________
___________![]() ,并补全条形图;
,并补全条形图;
(2)求本次调查获取的样本数据的平均数、众数和中位数;
(3)该区体育中考选报引体向上的男生共有1800人,如果体育中考引体向上达6个以上(含6个)得满分,请你估计该区体育中考中选报引体向上的男生能获得满分的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司生产并销售A,B两种品牌新型节能设备,第一季度共生产两种品牌设备20台,每台的成本和售价如下表:
品牌 | A | B |
成本价(万元/台) | 3 | 5 |
销售价(万元/台) | 4 | 8 |
设销售A种品牌设备x台,20台A,B两种品牌设备全部售完后获得利润y万元.(利润=销售价-成本)
(1)求y关于x的函数关系式;
(2)若生产两种品牌设备的总成本不超过80万元,那么公司如何安排生产A,B两种品牌设备,售完后获利最多?并求出最大利润;
(3)公司为营销人员制定奖励促销政策:第一季度奖金=公司总利润![]() 销售A种品牌设备台数
销售A种品牌设备台数![]() ,那么营销人员销售多少台A种品牌设备,获得奖励最多?最大奖金数是多少?
,那么营销人员销售多少台A种品牌设备,获得奖励最多?最大奖金数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高级酒店为了吸引顾客,设立了一个可以自由转动的转盘,如图所示,并规定:顾客消费100以上(不包括100元),就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准九折、八折、七折、五折区域顾客就可以获得此项待遇(转盘等分成16份).

(1)甲顾客消费80元,是否可获得转动转盘的机会?
(2)乙顾客消费150元,获得打折待遇的概率是多少?
(3)他获得九折,八折,七折,五折待遇的概率分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在证明定理“三角形的中位线平行于第三边,且等于第三边的一半”时,小明给出如下部分证明过程.
已知:在![]() 中,
中,![]() 分别是边
分别是边![]() 的中点.
的中点.
求证: .
证明:如图,延长![]() 到点
到点![]() ,使
,使![]() ,连接
,连接![]() ,
,
···
(1)补全求证:
(2)请根据添加的辅助线,写出完整的证明过程;
(3)若![]() 求边
求边![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com