
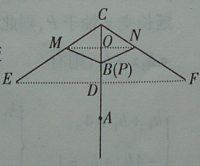
”¾ĢāÄæ”æČēĶ¼1ĖłŹ¾µÄÕŚŃōÉ”,É”±ś“¹Ö±ÓŚĖ®Ę½µŲĆę,ĘäŹ¾ŅāĶ¼ČēĶ¼2ĖłŹ¾,µ±É”ŹÕ½ōŹ±PÓėAÖŲŗĻ,µ±É”ĀżĀż³ÅæŖŹ±,¶ÆµćPÓÉAĻņBŅʶÆ,µ±µćPµ½“ļBŹ±,É”ÕŵĆ×īæŖ,“ĖŹ±×ī“óÕŽĒ”ĻECF=150”ć,ŅŃÖŖÉ”ŌŚ³ÅæŖµÄ¹ż³ĢÖŠ,×ÜÓŠPM=PN=CM=CN=6.0·ÖĆ×CE=CF=18.0·ÖĆ×.
(1)ĒóAP³¤µÄȔֵ·¶Ī§;
(2)µ±”ĻCPN=60”ć,ĒóAPµÄÖµ;
(3)ŌŚŃō¹ā“¹Ö±ÕÕÉäĻĀ,É”ÕŵĆ×īæŖŹ±,ĒóÉ”ĻĀµÄŅõÓ°(¼Ł¶ØĪŖŌ²Ćę)Ć껿S.(½į¹ū±£Įō![]() )(²Īæ¼Źż¾Ż:sin75”ć”Ö0.97,cos75”ć”Ö0.26,tan75”ć”Ö3.73)
)(²Īæ¼Źż¾Ż:sin75”ć”Ö0.97,cos75”ć”Ö0.26,tan75”ć”Ö3.73)

”¾“š°ø”æ£Ø1£©APµÄȔֵ·¶Ī§ĪŖ0”ÜAP”Ü8.88·ÖĆ×£»£Ø2£©AP=6·ÖĆ×£»£Ø3£©É”ĻĀŅõÓ°Ć껿ĪŖ![]() Ę½·½·ÖĆ×
Ę½·½·ÖĆ×
”¾½āĪö”æŹŌĢā·ÖĪö£ŗ
£Ø1£©ČēĻĀĶ¼£¬µ±µćPÓėµćBÖŲŗĻŹ±£¬AP×ī³¤£¬“ĖŹ±”ĻMCN=150”ć£¬Į¬½ÓMN½»BCÓŚµćO£¬ÓÉĢāŅāŅ×µĆĖıߊĪCMPNŹĒĮāŠĪ£¬ĄūÓĆĮāŠĪ¶Ō½ĒĻß»„Ļą“¹Ö±Ę½·ÖæɵƔĻCOM=75”ć£¬½įŗĻCM=6.0·ÖĆ×£¬æɽāµĆCO=1.56·ÖĆ×£¬“Ó¶ųæɵĆBC=3.12·ÖĆ×£¬ŌŁ½įŗĻAC=12·ÖĆ×æɵĆAB=8.88·ÖĆ×£¬ÓÉ“Ė¼“æɵƵ½![]() £»
£»
£Ø2£©µ±”ĻCPN=60”揱£¬½įŗĻPN=CN=6£¬æÉÖŖ”÷CPN“ĖŹ±ŹĒµČ±ßČż½ĒŠĪ£¬¹ŹCP=6£¬½įŗĻAC=12æɵƓĖŹ±AP=6·ÖĆ×£»
£Ø3£©ČēĻĀĶ¼£¬ÓÉĢāŅāæÉÖŖ£¬“ĖŹ±µćPÓėBÖŲŗĻ£¬Į¬½ÓEF½»ACÓŚµćD£¬ÓÉ£Ø1£©æÉÖŖMO=MC”¤sin”ĻMCO=5.82(·ÖĆ×)£¬“Ó¶ųæÉµĆ£ŗMN=11.64(·ÖĆ×)£¬ŌŁÖ¤”÷CMN”×”÷CEF¼“æɽįŗĻŅŃÖŖĒóµĆEFµÄ³¤£¬“Ó¶ų¼“æÉĒó³öĖłĒóĆ껿ĮĖ.
ŹŌĢā½āĪö£ŗ
(1)µ±µćPÓėBÖŲŗĻŹ±,AP×ī³¤,
“ĖŹ±”ĻMCN=1500
ČēĶ¼ĖłŹ¾£¬Į¬½ÓMN½»CBÓŚµćO£¬
”ßPM=PN=CM=CN=6.0·ÖĆ×,
”ąĖıߊĪCMPNŹĒĮāŠĪ£¬
”ąCB”ĶMN,¼“”ĻCOM=90”ć,”ĻMCO=![]() ”ĻMCN=75”ć£¬
”ĻMCN=75”ć£¬
ŌŚRt”÷MCOÖŠ,”ĻMCO=75”ć,CM=6.0·ÖĆ×,
”ąCO=CM”¤cos”ĻMCO=6.0”Į0.26=1.56(·ÖĆ×)£¬
”ąBC=2C0=3.12(·ÖĆ×)£¬
”ßAC=MC+MP=12(·ÖĆ×),
”ąAP=12-3.12=8.88(·ÖĆ×)£¬
”ąAPµÄȔֵ·¶Ī§ĪŖ0”ÜAP”Ü8.88·ÖĆ×£¬
(2)µ±”ĻCPN=60”揱,CP=CM=6·ÖĆ×,
”ąAP=6·ÖĆ×£»
(3)É”ÕÅæŖ×ī“óŹ±,µćPÓėBÖŲŗĻ,ČēĶ¼ĖłŹ¾,Į¬½ÓEF½»ACÓŚD£¬
ÓÉ(1)æɵĆMO=MC”¤sin”ĻMCO=6.0”Į0.97=5.82(·ÖĆ×)£¬
MN=2MO=11.64(·ÖĆ×)£¬
ŌŚ”÷CMNŗĶ”÷CEFÖŠ,”ĻMCN=”ĻECF,CM=CN,CE=CF£¬
”ą”÷CMN”×”÷CEF£¬
![]() £¬
£¬
µĆEF=34.92·ÖĆ×£¬
”ąÉ”ĻĀŅõÓ°Ć껿![]() (Ę½·½·ÖĆ×).
(Ę½·½·ÖĆ×).


 Š”Ģāæń×öĻµĮŠ“š°ø
Š”Ģāæń×öĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖÕż·½ŠĪABCDµÄ±ß³¤ĪŖ2£¬EŹĒ±ßBCÉĻµÄ¶Æµć£¬BF”ĶAE½»CDÓŚµćF£¬“¹×ćĪŖG£¬Į¬½įCG£®ĻĀĮŠĖµ·Ø£ŗ¢ŁAG£¾GE£»¢ŚAE=BF£»¢ŪµćGŌĖ¶ÆµÄĀ·¾¶³¤ĪŖ¦Š£»¢ÜCGµÄ×īŠ”ÖµĪŖ![]() ©1£®ĘäÖŠÕżČ·µÄĖµ·ØŹĒ £®£Ø°ŃÄćČĻĪŖÕżČ·µÄĖµ·ØµÄŠņŗŶ¼ĢīÉĻ£©
©1£®ĘäÖŠÕżČ·µÄĖµ·ØŹĒ £®£Ø°ŃÄćČĻĪŖÕżČ·µÄĖµ·ØµÄŠņŗŶ¼ĢīÉĻ£©

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĮāŠĪABCDÖŠ£¬µćEŹĒBC±ßµÄÖŠµć£¬¶ÆµćMŌŚCD±ßÉĻŌĖ¶Æ£¬ŅŌEMĪŖÕŪŗŪ½«”÷CEMÕŪµžµĆµ½”÷PEM£¬ĮŖ½ÓPA£¬ČōAB=4£¬”ĻBAD=60”ć£¬ŌņPAµÄ×īŠ”ÖµŹĒ£Ø””””£©
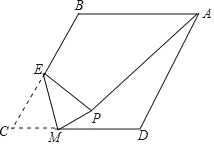
A. ![]() B. 2 C. 2
B. 2 C. 2![]() ©2 D. 4
©2 D. 4
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
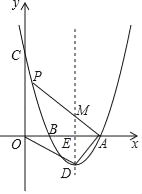
”¾ĢāÄæ”æČēĶ¼£¬Å×ĪļĻßy=mx2©8mx+12m£Øm£¾0£©ÓėxÖį½»ÓŚA£¬BĮ½µć£ØµćBŌŚµćAµÄ×ó²ą£©£¬ÓėyÖį½»ÓŚµćC£¬¶„µćĪŖD£¬Ęä¶Ō³ĘÖįÓėxÖį½»ÓŚµćE£¬ĮŖ½ÓAD£¬OD£®
£Ø1£©Ē󶄵ćDµÄ×ų±ź£ØÓĆŗ¬mµÄŹ½×Ó±ķŹ¾£©£»
£Ø2£©ČōOD”ĶAD£¬ĒóøĆÅ×ĪļĻßµÄŗÆŹż±ķ“ļŹ½£»
£Ø3£©ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬Éč¶ÆµćPŌŚ¶Ō³ĘÖį×ó²ąøĆÅ×ĪļĻßÉĻ£¬PAÓė¶Ō³ĘÖį½»ÓŚµćM£¬Čō”÷AMEÓė”÷OADĻąĖĘ£¬ĒóµćPµÄ×ų±ź£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æµćAŌŚŹżÖįÉĻ¶ŌÓ¦µÄŹżĪŖ3£¬µćB¶ŌÓ¦µÄŹżĪŖb£¬ĘäÖŠA”¢BĮ½µćÖ®¼äµÄ¾ąĄėĪŖ5
£Ø1£©ĒóbµÄÖµ
£Ø2£©µ±BŌŚA×ó²ąŹ±£¬Ņ»µćD“ÓŌµćO³ö·¢ŅŌĆæĆė2øöµ„Ī»µÄĖŁ¶ČĻņ×óŌĖ¶Æ£¬ĒėĪŹDŌĖ¶Æ¶ąÉŁŹ±¼ä£¬æÉŅŌŹ¹µĆDµ½A”¢BĮ½µćµÄ¾ąĄėÖ®ŗĶĪŖ8?
£Ø3£©µ±BŌŚAµÄ×ó²ąŹ±£¬Ņ»µćD“ÓO³ö·¢ŅŌĆæĆė2øöµ„Ī»µÄĖŁ¶ČĻņ×óŌĖ¶Æ£¬Ķ¬Ź±µćM“ÓB³ö·¢£¬ŅŌĆæĆė1øöµ„Ī»µÄĖŁ¶ČĻņ×óŌĖ¶Æ£¬µćN“ÓA³ö·¢£¬ŅŌĆæĆė4øöµ„Ī»µÄĖŁ¶ČĻņÓŅŌĖ¶Æ£»ŌŚŌĖ¶Æ¹ż³ĢÖŠ£¬MNµÄÖŠµćĪŖP£¬ODµÄÖŠµćĪŖQ£¬ĒėĪŹMN-2PQµÄÖµŹĒ·ń»į·¢Éś±ä»Æ£æČō·¢Éś±ä»Æ£¬ĒėĖµĆ÷ĄķÓÉ£»Čē¹ūƻӊ±ä»Æ£¬ĒėĒó³öÕāøöÖµ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼(1)ĖłŹ¾£¬EĪŖ¾ŲŠĪABCDµÄ±ßADÉĻŅ»µć£¬¶ÆµćP”¢QĶ¬Ź±“ÓµćB³ö·¢£¬µćPŅŌ1cm/ĆėµÄĖŁ¶ČŃŲÕŪĻßBE”ŖED”ŖDCŌĖ¶Æµ½µćCŹ±Ķ£Ö¹£¬µćQŅŌ2cm/ĆėµÄĖŁ¶ČŃŲBCŌĖ¶Æµ½µćCŹ±Ķ£Ö¹£®ÉčP”¢QĶ¬Ź±³ö·¢tĆėŹ±£¬”÷BPQµÄĆ껿ĪŖycm2£®ŅŃÖŖyÓėtµÄŗÆŹż¹ŲĻµĶ¼ĻóČēĶ¼(2)(ĘäÖŠĒśĻßOGĪŖÅ×ĪļĻßµÄŅ»²æ·Ö£¬ĘäÓąø÷²æ·Ö¾łĪŖĻ߶Ī)£¬ŌņĻĀĮŠ½įĀŪ£ŗ
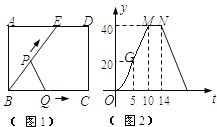
¢Łµ±0£¼t”Ü5Ź±£¬y£½![]() t2£»¢Śµ±t£½6ĆėŹ±£¬”÷ABE”Õ”÷PQB£»¢Ūcos”ĻCBE£½
t2£»¢Śµ±t£½6ĆėŹ±£¬”÷ABE”Õ”÷PQB£»¢Ūcos”ĻCBE£½![]() £»
£»
¢Üµ±t£½![]() ĆėŹ±£¬”÷ABE”×”÷QBP£»
ĆėŹ±£¬”÷ABE”×”÷QBP£»
ĘäÖŠÕżČ·µÄŹĒ£Ø £©
A£®¢Ł¢Ś B£®¢Ł¢Ū¢Ü C£®¢Ū¢Ü D£®¢Ł¢Ś¢Ü
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÄ³ÖŠŃ§¾ö¶ØÅÉ3Ćū½ĢŹ¦“ų![]() Ćūѧɜµ½Ä³·ē¾°Ēų¾ŁŠŠĻÄĮīÓŖ»ī¶Æ£¬¼×ĀĆŠŠÉēŹÕ·Ń±ź×¼ĪŖ½ĢŹ¦Č«Ę±£¬Ń§Éś°ė¼ŪÓÅ»Ż£»ŅŅĀĆŠŠÉēŹÕ·Ń±ź×¼ĪŖ½ĢŹ¦ŗĶѧɜȫ²æ°“ȫʱ¼ŪµÄ6ÕŪÓÅ»Ż.ŅŃÖŖ¼×”¢ŅŅĮ½ĀĆŠŠÉēµÄȫʱ¼Ū¾łĪŖ240ŌŖ.
Ćūѧɜµ½Ä³·ē¾°Ēų¾ŁŠŠĻÄĮīÓŖ»ī¶Æ£¬¼×ĀĆŠŠÉēŹÕ·Ń±ź×¼ĪŖ½ĢŹ¦Č«Ę±£¬Ń§Éś°ė¼ŪÓÅ»Ż£»ŅŅĀĆŠŠÉēŹÕ·Ń±ź×¼ĪŖ½ĢŹ¦ŗĶѧɜȫ²æ°“ȫʱ¼ŪµÄ6ÕŪÓÅ»Ż.ŅŃÖŖ¼×”¢ŅŅĮ½ĀĆŠŠÉēµÄȫʱ¼Ū¾łĪŖ240ŌŖ.
£Ø1£©ÓĆ“śŹżŹ½±ķŹ¾¼×”¢ŅŅĮ½ĀĆŠŠÉēµÄŹÕ·Ńø÷ŹĒ¶ąÉŁŌŖ£æ
£Ø2£©µ±![]() Ź±£¬Čē¹ūÄćŹĒŠ£³¤£¬ÄćŃ”ŌńÄÄŅ»¼ŅĀĆŠŠÉē£æ
Ź±£¬Čē¹ūÄćŹĒŠ£³¤£¬ÄćŃ”ŌńÄÄŅ»¼ŅĀĆŠŠÉē£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ÓÉÓŚø÷ČĖµÄĻ°¹ß²»Ķ¬£¬Ė«ŹÖ½»²ęŹ±×óŹÖ“óÄ“Öø»ņÓŅŹÖ“óÄ“ÖøŌŚÉĻŹĒŅ»øöĖ껜ŹĀ¼ž£¬ŌųĄĻŹ¦¶ŌĖūČĪ½ĢµÄѧɜ×öĮĖŅ»øöµ÷²é£¬Ķ³¼Ę½į¹ūČēĻĀ±ķĖłŹ¾£ŗ
2011½ģ | 2012½ģ | 2013½ģ | 2014½ģ | 2015½ģ | |
²ĪÓėŹµŃéµÄČĖŹż | 106 | 110 | 98 | 104 | 112 |
ÓŅŹÖ“óÄ“ÖøŌŚÉĻµÄČĖŹż | 54 | 57 | 49 | 51 | 56 |
ʵĀŹ | 0.509 | 0.518 | 0.500 | 0.490 | 0.500 |
øł¾Ż±ķøńÖŠµÄŹż¾Ż£¬ÄćČĻĪŖŌŚÕāøöĖ껜ŹĀ¼žÖŠ£¬ÓŅŹÖ“óÄ“ÖøŌŚÉĻµÄøÅĀŹæÉŅŌ¹Ą¼ĘĪŖ£Ø””””£©

A. 0.6 B. 0.5 C. 0.45 D. 0.4
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijŠ£¼Ę»®³ÉĮ¢ĻĀĮŠŃ§ÉśÉēĶÅ: A.ŗĻ³ŖĶÅ: B.Ó¢Óļ¾ćĄÖ²æ: C.¶ÆĀž““×÷Éē; D.ĪÄѧÉē:E.ŗ½Ä£¹¤×÷ŹŅĪŖĮĖ½āĶ¬Ń§ĆĒ¶ŌÉĻŹöѧɜÉēĶŵÄĻ²°®ĒéæöijæĪĢāŠ”×éŌŚČ«Š£Ń§ÉśÖŠĖ껜³éČ”ĮĖ²æ·ÖĶ¬Ń§£¬½ųŠŠ”°Äć×īĻ²°®µÄŅ»øöѧɜÉēĶÅ”±µÄµ÷²é£¬øł¾Żµ÷²é½į¹ū»ęÖĘĮĖČēĻĀÉŠ²»ĶźÕūµÄĶ³¼ĘĶ¼.
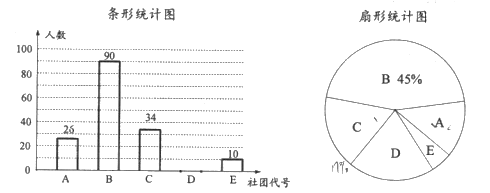
Ēėøł¾ŻŅŌÉĻŠÅĻ¢£¬½ā¾öĻĀĮŠĪŹĢā:
(1)±¾“Ī½ÓŹÜµ÷²éµÄѧɜ¹²ÓŠ¶ąÉŁČĖ;
(2)²¹Č«ĢõŠĪĶ³¼ĘĶ¼£¬ÉČŠĪĶ³¼ĘĶ¼ÖŠDŃ”ĻīĖł¶ŌÓ¦ÉČŠĪµÄŌ²ŠÄ½ĒĪŖ¶ąÉŁ£»
(3)ČōøĆѧŠ£¹²ÓŠŃ§Éś3000ČĖ£¬¹Ą¼ĘøĆѧŠ£Ń§ÉśÖŠĻ²°®ŗĻ³ŖĶÅŗĶ¶ÆĀž““×÷ÉēµÄ×ÜČĖŹż.
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com