
【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以M,N为圆心,大于 ![]() MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上;④S△DAC:S△ABC=1:3.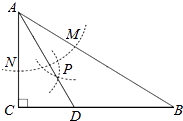
A.1
B.2
C.3
D.4
【答案】D
【解析】解:①根据作图的过程可知,AD是∠BAC的平分线.
故①正确;
②如图,∵在△ABC中,∠C=90°,∠B=30°,
∴∠CAB=60°.
又∵AD是∠BAC的平分线,
∴∠1=∠2= ![]() ∠CAB=30°,
∠CAB=30°,
∴∠3=90°﹣∠2=60°,即∠ADC=60°.
故②正确;
③∵∠1=∠B=30°,
∴AD=BD,
∴点D在AB的中垂线上.
故③正确;
④∵如图,在直角△ACD中,∠2=30°,
∴CD= ![]() AD,
AD,
∴BC=CD+BD= ![]() AD+AD=
AD+AD= ![]() AD,S△DAC=
AD,S△DAC= ![]() ACCD=
ACCD= ![]() ACAD.
ACAD.
∴S△ABC= ![]() ACBC=
ACBC= ![]() AC
AC ![]() AD=
AD= ![]() ACAD,
ACAD,
∴S△DAC:S△ABC= ![]() ACAD:
ACAD: ![]() ACAD=1:3.
ACAD=1:3.
故④正确.
综上所述,正确的结论是:①②③④,共有4个.
故选D.
①根据作图的过程可以判定AD是∠BAC的角平分线;
②利用角平分线的定义可以推知∠CAD=30°,则由直角三角形的性质来求∠ADC的度数;
③利用等角对等边可以证得△ADB的等腰三角形,由等腰三角形的“三合一”的性质可以证明点D在AB的中垂线上;
④利用30度角所对的直角边是斜边的一半、三角形的面积计算公式来求两个三角形的面积之比.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】“4000辆自行车、187个服务网点”,台州市区现已实现公共自行车服务全覆盖,为人们的生活带来了方便.图①是公共自行车的实物图,图②是公共自行车的车架示意图,点A、D、C、E在同一条直线上,CD=30cm,DF=20cm,AF=25cm,FD⊥AE于点D,座杆CE=15cm,且∠EAB=75°.
(1)求AD的长;
(2)求点E到AB的距离.(参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线 y=x2+2x+c 与 y 轴交点为(0,﹣3),则下列说法不正确的是( )
A. 抛物线开口向上 B. 当 x>﹣1 时,y 随 x 的增大而减小
C. 对称轴为 x=﹣1 D. c 的值为﹣3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小花最近买了三本课外书,分别是《汉语字典》用A表示,《流行杂志》用B表示和《故事大王》用C表示.班里的同学都很喜欢借阅,在五天内小花做了借书记录如下表:
书名 | 借阅 | |||||
星期一 | 星期二 | 星期三 | 星期四 | 星期五 | ||
A | 3 | 2 | 2 | 3 | 4 | 14 |
B | 4 | 3 | 3 | 2 | 3 | 15 |
C | 1 | 2 | 3 | 2 | 3 | 11 |
(1)在表中填写五天内每本书的借阅频数.
(2)计算五天内《汉语字典》的借阅频率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点坐标为 A(﹣3,0),B(﹣3,﹣3),C(﹣1,﹣3) 
(1)求Rt△ABC的面积;
(2)在图中作出△ABC关于x轴对称的图形△DEF,并写出D,E,F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为6,E是BC中点,将正方形边CD沿DE折叠到DF,将AD折叠,使AD与DF重合,折痕交AB于G,连接BF,CF,现在有如下4个结论:①G、F、E三点共线;②BG=4;③△BEF∽△CDF;④S△BFG=![]() .
.
在以上4个结论中,正确的有 ________________(填番号).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com