
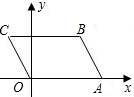
 如图,在OABC中OA=a,AB=b,∠AOC=120°,则点C、B的坐标分别为
如图,在OABC中OA=a,AB=b,∠AOC=120°,则点C、B的坐标分别为 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
 (2012•漳州)如图,在?OABC中,点A在x轴上,∠AOC=60°,0C=4cm.OA=8cm.动点P从点O出发,以1cm/s的速度沿线段OA→AB运动;动点Q同时从点O出发,以acm/s的速度沿线段OC→CB运动,其中一点先到达终点B时,另一点也随之停止运动.设运动时间为t秒.
(2012•漳州)如图,在?OABC中,点A在x轴上,∠AOC=60°,0C=4cm.OA=8cm.动点P从点O出发,以1cm/s的速度沿线段OA→AB运动;动点Q同时从点O出发,以acm/s的速度沿线段OC→CB运动,其中一点先到达终点B时,另一点也随之停止运动.设运动时间为t秒.| 3 |
| 3 |
| 7 |
| 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在?OABC中,O(0,0),A(2,2),C(4,0),写出一个能将该平行四边形分成面积相等的两部分的直线的解析式:
如图,在?OABC中,O(0,0),A(2,2),C(4,0),写出一个能将该平行四边形分成面积相等的两部分的直线的解析式:| 1 |
| 3 |
| 1 |
| 3 |
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(福建漳州卷)数学(带解析) 题型:解答题
如图,在 OABC中,点A在x轴上,∠AOC=60o,OC=4cm.OA=8cm.动点P从点O出发,以1cm/s的速度沿线段OA→AB运动;动点Q同时从点O出发,以acm/s的速度沿线段OC→CB运动,其中一点先到达终点B时,另一点也随之停止运动.设运动时间为t秒.
OABC中,点A在x轴上,∠AOC=60o,OC=4cm.OA=8cm.动点P从点O出发,以1cm/s的速度沿线段OA→AB运动;动点Q同时从点O出发,以acm/s的速度沿线段OC→CB运动,其中一点先到达终点B时,另一点也随之停止运动.设运动时间为t秒.
(1)填空:点C的坐标是(______,______),对角线OB的长度是_______cm;
(2)当a=1时,设△OPQ的面积为S,求S与t的函数关系式,并直接写出当t为何值时,S的值最大?
(3)当点P在OA边上,点Q在CB边上时,线段PQ与对角线OB交于点M.若以O、M、P为顶点的三角形与△OAB相似,求a与t的函数关系式,并直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(福建漳州卷)数学(解析版) 题型:填空题
如图,在 OABC中,点A在x轴上,∠AOC=60o,OC=4cm.OA=8cm.动点P从点O出发,以1cm/s的速度沿线段OA→AB运动;动点Q同时从点O出发,以acm/s的速度沿线段OC→CB运动,其中一点先到达终点B时,另一点也随之停止运动.设运动时间为t秒.
OABC中,点A在x轴上,∠AOC=60o,OC=4cm.OA=8cm.动点P从点O出发,以1cm/s的速度沿线段OA→AB运动;动点Q同时从点O出发,以acm/s的速度沿线段OC→CB运动,其中一点先到达终点B时,另一点也随之停止运动.设运动时间为t秒.
(1)填空:点C的坐标是(______,______),对角线OB的长度是_______cm;
(2)当a=1时,设△OPQ的面积为S,求S与t的函数关系式,并直接写出当t为何值时,S的值最大?
(3)当点P在OA边上,点Q在CB边上时,线段PQ与对角线OB交于点M.若以O、M、P为顶点的三角形与△OAB相似,求a与t的函数关系式,并直接写出t的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com