练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．化简根式：$\sqrt{4co{s}^{2}51°-4\sqrt{2}cos51°+2}$=$\sqrt{2}$-2cos51°．

    分析 原式被开方数利用完全平方公式化简，再利用二次根式性质及绝对值的代数意义化简即可得到结果．

    解答 解：∵cos51°＜cos45°=$\frac{\sqrt{2}}{2}$，∴2cos51°-$\sqrt{2}$＜0，
    则原式=$\sqrt{（2cos51°-\sqrt{2}）^{2}}$=|2cos51°-$\sqrt{2}$|=$\sqrt{2}$-2cos51°．
    故答案为：$\sqrt{2}$-2cos51°

    点评 此题考查了二次根式的性质与化简，以及绝对值的代数意义，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    12．用配方法解方程x2+4x+1=0，配方后的方程是（　　）
    A．（x-2）2=5B．（x+2）2=5C．（x+2）2=3D．（x-2）2=3

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

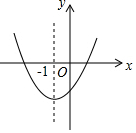    13．已知二次函数y=ax2+bx+c的图象如图所示，其对称轴方程为x=-1，给出下列结果：①b2＞4ac；②abc＞0；③2a+b=0；④a+b+c＞0；⑤a-b+c＜0，则正确的结论是（　　）
    A．①②③④B．②④⑤C．①④⑤D．②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．计算：
    （1）-1+5÷（-$\frac{1}{4}$）×4；
    （2）32×（-$\frac{1}{3}$）+8÷（-2）2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．如图，△ABC和△CDE都是等边三角形，点A、E、D在同一条直线上，且∠EBD=62°，求∠AEB的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．如图，CA=CB，CD=CE，∠ACB=∠DCE=α，连AD，BE相交于H，连CH
    （1）如图1，当α=60°时，求∠AHE与∠BHC；
    （2）如图2，当α=90°时，求∠AHE与∠BHC；
    （3）如图3，当α为锐角时，求∠AHE与∠BHC；
    （4）如图4，当α为钝角时，求∠AHE与∠BHC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．我们规定以下三种变换：
    （1）f（a，b）=（-a，b）．如：f（1，3）=（-1，3）；
    （2）g（a，b）=（b，a）．如：g（1，3）=（3，1）；
    （3）h（a，b）=（-a，-b）．如：h（1，3）=（-1，-3）．
    按照以上变换有：f（g（2，-3））=f（-3，2）=（3，2），
    求f（h（5，-3））=（　　）
    A．（5，-3）B．（-5，3）C．（5，3）D．（3，5）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

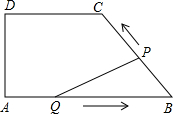    3．如图，在四边形ABCD中，DC∥AB，AD=4，DC=5，AB=8．如果点P由B点出发沿BC方向向点C匀速运动，同时点Q由A点出发沿AB方向向点B匀速运动，它们的速度均为每秒1个单位长度．当P点到达C点时，两点同时停止运动，连接PQ．设运动时间为t秒，当△PQB为等腰三角形时，t的值为$\frac{40}{11}$、$\frac{48}{11}$或4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．如图，在△ABC中，AB=AC=2BC，以点B为圆心，BC长为半径作弧，与AC交于点D．若AC=4，则线段CD的长为1．

    查看答案和解析>>

    同步练习册答案