
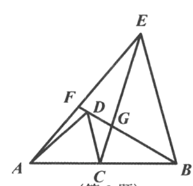
【题目】如图,在线段AB上有一点C,在AB的同侧作等腰△ACD和等腰△ECB,且AC=AD,EC=EB,∠DAC=∠CEB,直线BD与线段AE,线段CE分别交于点F,G.对于下列结论:①△DCG∽△BEG;②△ACE∽△DCB;③GF·GB=GC·GE;④若∠DAC=∠CEB=90°,则2AD2=DF·DG.其中正确的是( )
A.①②③④B.①②③C.①③④D.①②
【答案】A
【解析】
利用三角形的内角和定理及两组角分别相等证明①正确;根据两组边成比例夹角相等判断②正确;利用③的相似三角形证得∠AEC=∠DBC,又对顶角相等,证得③正确;根据△ACE∽△DCB证得F、E、B、C四点共圆,由此推出△DCF∽△DGC,列比例线段即可证得④正确.
①正确;在等腰△ACD和等腰△ECB中AC=AD,EC=EB,∠DAC=∠CEB,
∴∠ACD=∠ADC=∠BCE=∠BEC,
∴∠DCG=180![]() -∠ACD-∠BCE=∠BEC,
-∠ACD-∠BCE=∠BEC,
∵∠DGC=∠BGE,
∴△DCG∽△BEG;
②正确;∵∠ACD+∠DCG=∠BCE+∠DCG,
∴∠ACE=∠DCB,
∵![]() ,
,
∴△ACE∽△DCB;
③正确;∵△ACE∽△DCB,
∴∠AEC=∠DBC,
∵∠FGE=∠CGB,
∴△FGE∽△CGB,
∴GF·GB=GC·GE;
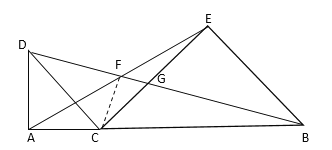
④正确;如图,连接CF,
由②可得△ACE∽△DCB,
∴∠AEC=∠DBC,
∴F、E、B、C四点共圆,
∴∠CFB=∠CEB=90![]() ,
,
∵∠ACD=∠ECB=45![]() ,
,
∴∠DCE=90![]() ,
,
∴△DCF∽△DGC
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴2AD2=DF·DG.
故选:A.


科目:初中数学 来源: 题型:
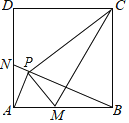
【题目】如图,在正方形ABCD中,N为边AD上一点,连接BN.过点A作AP⊥BN于点P,连接CP,M为边AB上一点,连接PM,∠PMA=∠PCB,连接CM,有以下结论:①△PAM∽△PBC;②PM⊥PC;③M、P、C、B四点共圆;④AN=AM.其中正确的个数为( )
A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一小球沿与地面成一定角度的方向飞出,小球的飞行路线是一条抛物线,如果不考虑空气阻力,小球的飞行高度y(单位:m)与飞行时间x(单位:s)之间具有函数关系y=﹣5x2+20x,请根据要求解答下列问题:
(1)在飞行过程中,当小球的飞行高度为15m时,飞行时间是多少?
(2)在飞行过程中,小球从飞出到落地所用时间是多少?
(3)在飞行过程中,小球飞行高度何时最大?最大高度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2-4ax+4(a≠0)与y轴交于点A.过点B(0,3)作y轴的垂线l,若抛物线y=ax2-4ax+4(a≠0)与直线l有两个交点,设其中靠近y轴的交点的横坐标为m,且│m│<1,则a的取值范围是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
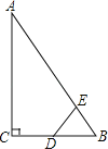
【题目】如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=4cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<12),连接DE,当△BDE是直角三角形时,t的值为( )
A.4或5B.4或7C.4或5或7D.4或7或9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习概率的课堂上,老师提出的问题:只有一张电影票,小丽和小芳想通过抽取扑克牌的游戏来决定谁去看电影,请你设计一个对小丽和小芳都公平的方案.甲同学的方案:将红桃2、3、4、5四张牌背面向上,小丽先抽一张,小芳从剩下的三张牌中抽一张,若两张牌上的数字之和是奇数,则小丽看电影,否则小芳看电影.
(1)甲同学的方案公平吗?请用列表或画树状图的方法说明;
(2)乙同学将甲同学的方案修改为只用2、3、5、7四张牌,抽取方式及规则不变,乙的方案公平吗?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
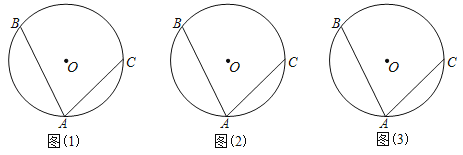
【题目】作图题:⊙O上有三个点A,B,C,∠BAC=70°,请画出要求的角,并标注.
(1)画一个140°的圆心角;(2)画一个110°的圆周角;(3)画一个20°的圆周角.
查看答案和解析>>
科目:初中数学 来源: 题型:
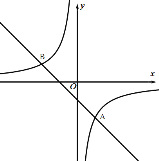
【题目】如图,一次函数的图象![]() 与反比例函数的图象
与反比例函数的图象![]() 交于A(2,﹣4),B(m, 2)两点.当x满足条件______________时,一次函数的值大于反比例函数值.
交于A(2,﹣4),B(m, 2)两点.当x满足条件______________时,一次函数的值大于反比例函数值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com