
(本题满分10分)如图,在同一平面内,两条平行高速公路l1和l2间有一条“Z”型道路连通,其中AB段与高速公路l1成30°角,长为20km;BC段与AB、CD段都垂直,长为10km,CD段长为30km,求两高速公路间的距离(结果保留根号).

25+5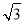 km
km
【解析】
试题分析:过点A作AB的垂线交DC延长线于点E,过点E作l1的垂线与l1、l2分别交于点H,F,则HF⊥l2.根据条件可证四边形ABCE是矩形,从而DE=DC+CE=DC+AB=50.在Rt△DEF中,根据三角函数求得EF,在Rt△AEH中,根据三角函数求得EH,再根据HF=EF+HE即可求解.
试题解析:如图,过点A作AB的垂线交DC延长线于点E,过点E作l1的垂线与l1、l2分别交于点H,F,则HF⊥l2.

由题意知AB⊥BC,BC⊥CD,又AE⊥AB,
∴四边形ABCE是矩形.∴AE=BC,AB=EC.
∴DE=DC+CE=DC+AB=50.
又AB与l1成30°角,∴∠EDF=30°,∠EAH=60°.
在Rt△DEF中,EF=DEsin30°=50×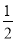 =25.
=25.
在Rt△AEH中,EH=AEsin60°=10×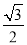 =5
=5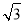 ,
,
所以HF=EF+HE=25+5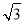 km.
km.
考点:解直角三角形的应用.
考点分析: 考点1:函数基础知识 函数的定义:

 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源:2014-2015学年江苏省扬州市片九年级3月月考数学试卷(解析版) 题型:解答题
(本题满分10分)抛物线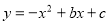 与x轴交与
与x轴交与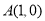 ,
,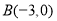 两点,
两点,
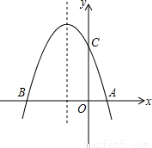
(1)求该抛物线的解析式;
(2)设(1)中的抛物线与y轴交于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省联盟九年级下学期第一次月考数学试卷(解析版) 题型:解答题
(10分)如图,已知△ABC是等腰三角形,顶角∠BAC=α(α<60°),D是BC边上的一点,连接AD,线段AD绕点A顺时针旋转α到AE,过点E作BC的平行线,交AB于点F,连接DE,BE,DF.
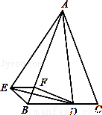
(1)求证:BE=CD;
(2)若AD⊥BC,试判断四边形BDFE的形状,并给出证明.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市九年级4月阶段检测数学试卷(解析版) 题型:选择题
下列二次函数中,图象以直线x=2为对称轴、且经过点(0,1)的是 ( )
A.y=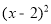 +1 B.y=
+1 B.y=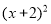 +1
+1
C.y=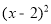 -3 D.y=
-3 D.y=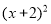 -3
-3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com