
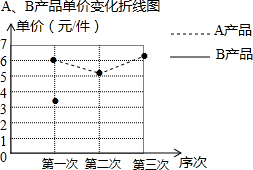
 某厂生产A,B两种产品,其单价随市场变化而做相应调整.营销人员根据前三次单价变化的情况,绘制了单价变化不完整的统计表及折线图.
某厂生产A,B两种产品,其单价随市场变化而做相应调整.营销人员根据前三次单价变化的情况,绘制了单价变化不完整的统计表及折线图.| 第一次 | 第二次 | 第三次 | |
| A产品单价(元/件) | 6 | 5.2 | 6.5 |
| B产品单价(元/件) | 3.5 | 4 | 3 |
分析 (1)根据题目提供数据补充折线统计图即可;
(2)分别计算平均数及方差即可;
(3)首先确定这四次单价的中位数,然后确定第四次调价的范围,根据“A产品这四次单价的中位数是B产品四次单价中位数的2倍少1”列式求m即可.
解答 解:(1)如图2所示: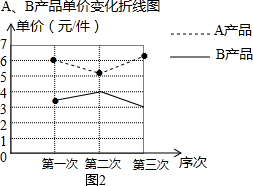
(2)$\overline{{x}_{B}}$=$\frac{1}{3}$(3.5+4+3)=3.5,S${{\;}_{B}}^{2}$=$\frac{(3.5-3.5)^{2}+(4-3.5)^{2}+(3-3.5)^{2}}{3}$=$\frac{1}{6}$,
∵B产品的方差小,
∴B产品的单价波动小;
(3)第四次调价后,对于A产品,这四次单价的中位数为$\frac{6+6.5}{2}$=$\frac{25}{4}$;
对于B产品,∵m>0,
∴第四次单价大于3,
∵第四次单价小于4,
∴$\frac{3(1+m%)+3.5}{\;}$×2-1=$\frac{25}{4}$,
∴m=25.
点评 本题考查了方差、条形统计图、算术平均数、中位数的知识,解题的关键是根据方差公式进行有关的运算,难度不大.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{8}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{9}$ | D. | $\frac{32}{27}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
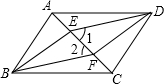 (1)如图,四边形ABCD是平行四边形,BE∥DF,且分别交对角线AC于点E,F,连接ED,BF.求证:∠1=∠2.
(1)如图,四边形ABCD是平行四边形,BE∥DF,且分别交对角线AC于点E,F,连接ED,BF.求证:∠1=∠2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
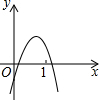 y=ax2+bx+c的图象如图所示,则下面结论中正确的结论有( )
y=ax2+bx+c的图象如图所示,则下面结论中正确的结论有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com