
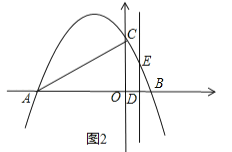
【题目】如图,抛物线![]() 与x轴交于两点A(﹣4,0)和B(1,0),与y轴交于点C(0,2),动点D沿△ABC的边AB以每秒2个单位长度的速度由起点A向终点B运动,过点D作x轴的垂线,交△ABC的另一边于点E,将△ADE沿DE折叠,使点A落在点F处,设点D的运动时间为t秒.
与x轴交于两点A(﹣4,0)和B(1,0),与y轴交于点C(0,2),动点D沿△ABC的边AB以每秒2个单位长度的速度由起点A向终点B运动,过点D作x轴的垂线,交△ABC的另一边于点E,将△ADE沿DE折叠,使点A落在点F处,设点D的运动时间为t秒.
(1)求抛物线的解析式和对称轴;
(2)是否存在某一时刻t,使得△EFC为直角三角形?若存在,求出t的值;若不存在,请说明理由;
(3)设四边形DECO的面积为s,求s关于t的函数表达式.

【答案】(1)![]() ,对称轴为:直线x=﹣
,对称轴为:直线x=﹣![]() ;(2)t=
;(2)t=![]() 或
或![]() ;(3)
;(3)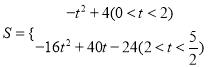 .
.
【解析】试题分析:(1)把A(﹣4,0),B(1,0),点C(0,2)即可得到结论;
(2)由题意得AD=2t,DF=AD=2t,OF=4﹣4t,由于直线AC的解析式为: ![]() ,得到E(2t﹣4,t),①当∠EFC=90°,则△DEF∽△OFC,根据相似三角形的性质得到结论;②当∠FEC=90°,根据等腰直角三角形的性质得到结论;③当∠ACF=90°,根据勾股定理得到结论;
,得到E(2t﹣4,t),①当∠EFC=90°,则△DEF∽△OFC,根据相似三角形的性质得到结论;②当∠FEC=90°,根据等腰直角三角形的性质得到结论;③当∠ACF=90°,根据勾股定理得到结论;
(3)求得直线BC的解析式为:y=﹣2x+2,当D在y轴的左侧时,当D在y轴的右侧时,如图2,根据梯形的面积公式即可得到结论.
试题解析:解:(1)把A(﹣4,0),B(1,0),点C(0,2)代入![]() 得:
得: 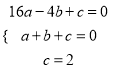 ,解得:
,解得:  ,∴抛物线的解析式为:
,∴抛物线的解析式为: ![]() ,对称轴为:直线x=﹣
,对称轴为:直线x=﹣![]() ;
;
(2)存在,∵AD=2t,∴DF=AD=2t,∴OF=4﹣4t,∴D(2t﹣4,0),∵直线AC的解析式为: ![]() ,∴E(2t﹣4,t),∵△EFC为直角三角形,分三种情况讨论:
,∴E(2t﹣4,t),∵△EFC为直角三角形,分三种情况讨论:
①当∠EFC=90°,则△DEF∽△OFC,∴ ![]() ,即
,即![]() ,解得:t=
,解得:t=![]() ;
;
②当∠FEC=90°,∴∠AEF=90°,∴△AEF是等腰直角三角形,∴DE=![]() AF,即t=2t,∴t=0,(舍去),③当∠ACF=90°,则AC2+CF2=AF2,即(42+22)+[22+(4t﹣4)2]=(4t)2,解得:t=
AF,即t=2t,∴t=0,(舍去),③当∠ACF=90°,则AC2+CF2=AF2,即(42+22)+[22+(4t﹣4)2]=(4t)2,解得:t=![]() ,∴存在某一时刻t,使得△EFC为直角三角形,此时,t=
,∴存在某一时刻t,使得△EFC为直角三角形,此时,t=![]() 或
或![]() ;
;
(3)∵B(1,0),C(0,2),∴直线BC的解析式为:y=﹣2x+2,当D在y轴的左侧时,S=![]() (DE+OC)OD=
(DE+OC)OD=![]() (t+2)(4﹣2t)=﹣t2+4 (0<t<2);
(t+2)(4﹣2t)=﹣t2+4 (0<t<2);
当D在y轴的右侧时,如图2,∵OD=4t﹣4,DE=﹣8t+10,S=![]() (DE+OC)OD=
(DE+OC)OD=![]() (﹣8t+10+2)(4t﹣4),即
(﹣8t+10+2)(4t﹣4),即![]() (2<t<
(2<t<![]() ).
).
综上所述: 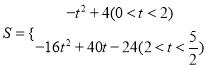


科目:初中数学 来源: 题型:
【题目】“富春包子”是扬州特色早点,富春茶社为了了解顾客对各种早点的喜爱情况,设计了如右图的调查问卷,对顾客进行了抽样调查.根据统计数据绘制了如下尚不完整的统计图.

根据以上信息,解决下列问题:
(1)条形统计图中“汤包”的人数是 ,扇形统计图中“蟹黄包”部分的圆心角为 °;
(2)根据抽样调查结果,请你估计富春茶社1000名顾客中喜欢“汤包”的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中:①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.不正确的有( )
A.①②B.②③C.②④D.④③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】坐火车从上海到娄底,高铁G1329次列车比快车K575次列车少需要9小时,已知上海到娄底的铁路长约1260千米,G1329的平均速度是K575的2.5倍.
(1)求K575的平均速度;
(2)高铁G1329从上海到娄底只需几小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是()
A. 正数与负数互为相反数
B. 符号不同的两个数互为相反数
C. 数轴上原点两旁的两个点所表示的数互为相反数
D. 任何一个有理数都有它的相反数
查看答案和解析>>
科目:初中数学 来源: 题型:
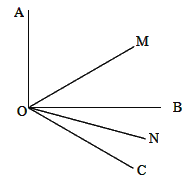
【题目】如图,∠AOB=90°,∠BOC=60°,射线OM平分∠AOC,ON平分∠BOC。
(1)求∠MON的度数;
(2)如果(1)中,∠AOB=α,∠BOC=β(β为锐角),其他条件不变,求∠MON的度数;
(3)从(1)、(2)的结果中,你能得到什么规律?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com