
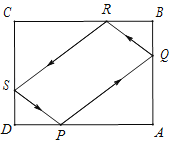
【题目】如图ABCD是一个矩形桌子,一小球从P撞击到Q,反射到R,又从R反射到S,从S反射回原处P,入射角与反射角相等(例如∠PQA=∠RQB等),已知AB=9,BC=12,BR=4.则小球所走的路径的长为_____.
【答案】30.
【解析】
证明四边形SPQR是平行四边形,推出SR=PQ,PS=QR,证三角形全等得出SR=PQ,RQ=PS,根据相似求出DS,根据勾股定理求出即RS,RQ,PQ,SP即可.
解:∵入射角与反射角相等,
∴∠BQR=∠AQP,∠APQ=∠SPD,∠CSR=∠DSP,∠CRS=∠BRQ,
∵四边形ABCD是矩形,
∴∠A=∠B=∠C=∠D=90°,
∴∠DPS+∠DSP=90°,∠AQP+∠APQ=90°,
∴∠DSP=∠AQP=∠CSR=∠BQR,
∴∠RSP=∠RQP,
同理∠SRQ=∠SPQ,
∴四边形SPQR是平行四边形,
∴SR=PQ,PS=QR,
在△DSP和△BQR中
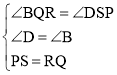 ,
,
∴△DSP≌△BQR(AAS),
∴BR=DP=4,BQ=DS,
∵四边形ABCD是矩形,
AB=CD=9,BC=AD=112,
∴AQ=9﹣DS,AP=12﹣4=8,
∵∠SPD=∠APQ,
∴△SDP∽△QAP,
![]() ,
,
![]() ,
,
∴DS=3,
在Rt△DSP中,由勾股定理得:PS=QR=![]() ,
,
同理PQ=RS=10,
∴QP+PS+SR+QR=2×5+2×10=30,
故答案为:30.


科目:初中数学 来源: 题型:
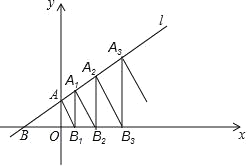
【题目】如图,在平面直角坐标系中,点A,A1,A2,A3…An都在直线1:y=![]() x+1上,点B,B1,B2,B3…Bn都在x轴上,且AB1⊥1,B1A1⊥x轴,A1B2⊥1,B2A2⊥x轴,则An的横坐标为_________(用含有n的代数式表示)。
x+1上,点B,B1,B2,B3…Bn都在x轴上,且AB1⊥1,B1A1⊥x轴,A1B2⊥1,B2A2⊥x轴,则An的横坐标为_________(用含有n的代数式表示)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一个三位数,它的各个数位上的数字都不为零,且满足百位上的数字与个位上的数字的平均数等于十位上的数字,则称这个三位数为开合数.设![]() 为一个开合数,将
为一个开合数,将![]() 的百位数字与个位数字交换位置后得到的新数再与
的百位数字与个位数字交换位置后得到的新数再与![]() 相加的和记为
相加的和记为![]() .例如:852是“开合数”,则
.例如:852是“开合数”,则![]() .
.
(1)已知开合数![]() (
(![]() ,且为
,且为![]() 整数),求
整数),求![]() 的值;
的值;
(2)三位数![]() 是一个开合数,若百位数字小于个位数字,
是一个开合数,若百位数字小于个位数字,![]() 是一个整数,且
是一个整数,且![]() 能被个位数字与百位数字的差整除,请求满足条件的所有
能被个位数字与百位数字的差整除,请求满足条件的所有![]() 值.
值.
查看答案和解析>>
科目:初中数学 来源: 题型:
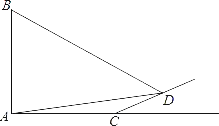
【题目】如图,旗杆AB的顶端B在夕阳的余辉下落在一个斜坡上的点D处,某校数学课外兴趣小组的同学正在测量旗杆的高度,在旗杆的底部A处测得点D的仰角为15°,AC=10米,又测得∠BDA=45°.已知斜坡CD的坡度为i=1:![]() ,求旗杆AB的高度(
,求旗杆AB的高度(![]() ,结果精确到个位).
,结果精确到个位).
查看答案和解析>>
科目:初中数学 来源: 题型:
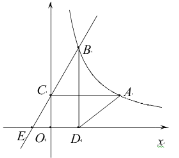
【题目】如图,已知反比例函数![]() 的图象经过点
的图象经过点![]() ,过
,过![]() 作
作![]() 轴于点
轴于点![]() .点
.点![]() 为反比例函数图象上的一动点,过点
为反比例函数图象上的一动点,过点![]() 作
作![]() 轴于点
轴于点![]() ,连接
,连接![]() .直线
.直线![]() 与
与![]() 轴的负半轴交于点
轴的负半轴交于点![]() .
.
(1)求反比例函数的表达式;
(2)若![]() ,求
,求![]() 的面积;
的面积;
(3)是否存在点![]() ,使得四边形
,使得四边形![]() 为平行四边形?若存在,请求出点
为平行四边形?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班为参加学校的大课间活动比赛,准备购进一批跳绳,已知2根![]() 型跳绳和1根
型跳绳和1根![]() 型跳绳共需56元,1根
型跳绳共需56元,1根![]() 型跳绳和2根
型跳绳和2根![]() 型跳绳共需82元.
型跳绳共需82元.
(1)求一根![]() 型跳绳和一根
型跳绳和一根![]() 型跳绳的售价各是多少元?
型跳绳的售价各是多少元?
(2)学校准备购进这两种型号的跳绳共50根,并且![]() 型跳绳的数量不多于
型跳绳的数量不多于![]() 型跳绳数量的3倍,请设计出最省钱的购买方案,并说明理由.
型跳绳数量的3倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系xOy中,半径为1的⊙O与x轴正半轴和y轴正半轴分别交于A,B两点,直线l:y=kx+2(k<0)与x轴和y轴分别交于P,M两点.
(1)当直线与⊙O相切时,求出点M的坐标和点P的坐标;
(2)如图2,当点P在线段OA上时,直线1与⊙O交于E,F两点(点E在点F的上方)过点F作FC∥x轴,与⊙O交于另一点C,连结EC交y轴于点D.
①如图3,若点P与点A重合时,求OD的长并写出解答过程;
②如图2,若点P与点A不重合时,OD的长是否发生变化,若不发生变化,请求出OD的长并写出解答过程;若发生变化,请说明理由.
(3)如图4,在(2)的基础上,连结BF,将线段BF绕点B逆时针旋转90°到BQ,若点Q在CE的延长线时,请用等式直接表示线段FC,FQ之间的数量关系.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com