
【题目】在创建文明城区的活动中,有两端长度相等的彩色道砖铺设任务,分别交给甲、乙两个施工队同时进行施工.如图是反映所铺设彩色道砖的长度![]() (米)与施工时间
(米)与施工时间![]() (时)之间的关系的部分图像.请解答下列问题.
(时)之间的关系的部分图像.请解答下列问题.
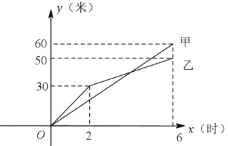
(1)甲队在![]() 的时段内的速度是 米/时.乙队在
的时段内的速度是 米/时.乙队在![]() 的时段内的速度是 米/时. 6小时甲队铺设彩色道砖的长度是 米,乙队铺设彩色道砖的长度是 米.
的时段内的速度是 米/时. 6小时甲队铺设彩色道砖的长度是 米,乙队铺设彩色道砖的长度是 米.
(2)如果铺设的彩色道砖的总长度为150米,开挖6小时后,甲队、乙队均增加人手,提高了工作效率,此后乙队平均每小时比甲队多铺5米,结果乙反而比甲队提前1小时完成总铺设任务.求提高工作效率后甲队、乙队每小时铺设的长度分别为多少米?
【答案】(1)10, 5, 60, 50;(2)提高工作效率后甲队每小时铺设的长度分别为15米、乙队每小时铺设的长度为20米.
【解析】
(1)根据函数图象,速度=路程÷时间,即可解答;
(2)根据题意列方程解答即可.
解:(1)(1)由图象可得,
甲队在0≤x≤6的时段内的速度是:60÷6=10(米/时);
乙队在2≤x≤6的时段内的速度是:(5030)÷(62)=5(米/时);
6小时甲队铺设彩色道砖的长度是60米,乙队铺设彩色道砖的长度是50米.
故答案为:10;5;60;50;
(2)设提高工作效率后甲队每小时铺设的长度分别为![]() 米,由题意得:
米,由题意得:
![]() ,
,
整理得:![]() ,
,
解得:![]() ,
, ![]()
经检验:![]() ,
,![]() 都是原方程的解,
都是原方程的解,![]() 不合题意,舍去.
不合题意,舍去.
答:提高工作效率后甲队每小时铺设的长度分别为15米、乙队每小时铺设的长度为20米.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某校组织了主题为“让勤俭节约成为时尚”的电子小组作品征集活动,现从中随机抽取部分作品,对其份数和成绩(十分制)进行整理,制成了如下两幅不完整的统计图.
(1)求本次抽取的作品数量并补全条形统计图;
(2)此次被抽取的作品的平均得分是分.
(3)若该校共征集到800份作品,请估计8分的作品约有多少份?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,矩形OABC的两条边OA、OC分别在y轴和x轴上,已知点A(0,3)、点C(-4,0).
(1)若把矩形OABC沿直线DE折叠,使点C落在点A处,直线DE与OC、AC、AB的交点分别为D、F、E,求折痕DE的长;
(2)若点P在x轴上,在平面内是否存在点Q,使以P、D、E、Q为顶点的四边形是菱形?若存在,则请直接写出点Q的坐标;若不存在,请说明理由;
(3)如图2,若M为AC边上的一动点,在OA上取一点N(0,1),将矩形OABC绕点O顺时针旋转一周,在旋转的过程中,M的对应点为M1,请直接写出NM1的最大值和最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上点![]() 表示的数为6,点
表示的数为6,点![]() 位于
位于![]() 点的左侧,
点的左侧,![]() ,动点
,动点![]() 从点
从点![]() 出发,以每秒3个单位长度的速度沿数轴向左运动,动点
出发,以每秒3个单位长度的速度沿数轴向左运动,动点![]() 从点
从点![]() 出发,以每秒2个单位长度的速度沿数轴向右运动.
出发,以每秒2个单位长度的速度沿数轴向右运动.
(1)点![]() 表示的数是多少?
表示的数是多少?
(2)若点![]() ,
,![]() 同时出发,求:
同时出发,求:
①当点![]() 与
与![]() 相遇时,它们运动了多少秒?相遇点对应的数是多少?
相遇时,它们运动了多少秒?相遇点对应的数是多少?
②当![]() 个单位长度时,它们运动了多少秒?
个单位长度时,它们运动了多少秒?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在南通市中小学标准化建设工程中,某校计划购进一批电脑和电子白板,经过市场考察得知,购买![]() 台电脑和
台电脑和![]() 台电子白板需要
台电子白板需要![]() 万元,购买
万元,购买![]() 台电脑和
台电脑和![]() 台电子白板需要
台电子白板需要![]() 万元.
万元.
(1)求每台电脑、每台电子白板各多少万元;
(2)根据学校实际,需购进电脑和电子白板共![]() 台,若总费用不超过
台,若总费用不超过![]() 万元,则至多购买电子白板多少台?
万元,则至多购买电子白板多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一天,小明和小玲玩纸片拼图游戏,发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式,比如图②可以解释为:![]()
(1)图③可以解释为等式: .
(2)要拼出一个长为a+3b,宽为2a+b的长方形,需要如图所示![]() 块,
块,![]() 块,
块,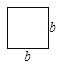 块.
块.
(3)如图④,大正方形的边长为m,小正方形的边长为n,若用x、y表示四个小长方形的两边长(x>y),观察图案,以下关系式正确的是 (填序号).
①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在平面直角坐标系中,![]() 的顶点坐标分别
的顶点坐标分别![]() ,现将
,现将![]() 先向右平移6个单位长度,再向下平移5个单位长度,得到
先向右平移6个单位长度,再向下平移5个单位长度,得到![]() .
.

(1)直接写出点![]() 的坐标;
的坐标;
(2)在平面直角坐标中画出![]() ,并求出
,并求出![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com