
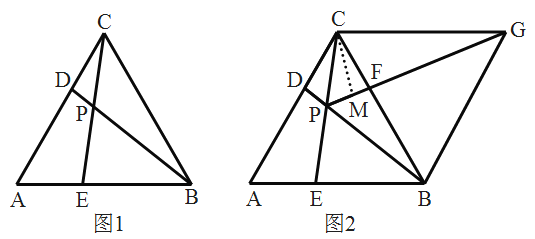
【题目】如图,![]() 是等边三角形,点
是等边三角形,点![]() ,
,![]() 分别在
分别在![]() 上,且
上,且![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() .
.
(1)求证:![]() ;
;
(2)如图2,将![]() 沿直线
沿直线![]() 翻折得到对应的
翻折得到对应的![]() ,过点
,过点![]() 作
作![]() ,交射线
,交射线![]() 于点
于点![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() .
.
①试判断四边形![]() 的形状,并说明理由.
的形状,并说明理由.
②若四边形![]() 的面积为
的面积为![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)①四边形![]() 为菱形,理由见解析,②CE=3
为菱形,理由见解析,②CE=3
【解析】
(1)根据SAS证明:△ACE≌△CBD;(2)①根据(1)中:△ACE≌△CBD,得∠ACE=∠CBD,则∠DPC=∠ACB=60°,证明△CDB≌△CFG,可得CG=AB=AC,则四边形ABGC是菱形;②作高CH,设菱形ABGC的边长为a,根据菱形的面积列式为:ABCH=6![]() ,即a
,即a![]() a=6
a=6![]() ,可得a的值,证明△BGF∽△PGB,列比例式可得FG的长,由△CDB≌△CFG,△ACE≌△CBD,根据对应边相等可得结论.
,可得a的值,证明△BGF∽△PGB,列比例式可得FG的长,由△CDB≌△CFG,△ACE≌△CBD,根据对应边相等可得结论.
(1)证明:
![]() 是等边三角形,
是等边三角形,
![]() ,
,![]() .
.
又![]() ,
,
![]() .
.
(2)解:①四边形![]() 为菱形,理由如下:
为菱形,理由如下:
![]()
![]()
![]()
由翻折可知:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 四边形
四边形![]() 为平行四边形.
为平行四边形.
![]() ,
,
![]() 平行四边形
平行四边形![]() 为菱形.
为菱形.
图2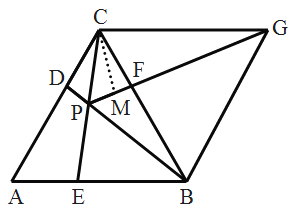
②过![]() 作
作![]() 于点
于点![]() .
.
设菱形![]() 的边长为
的边长为![]() .
.
![]() 为等边三角形,
为等边三角形,
![]()
![]()
![]()
![]() 菱形
菱形![]() 的面积为
的面积为![]() ,
,
![]() ,即
,即![]() .
.
![]()
![]()
![]() 四边形
四边形![]() 是菱形,
是菱形,
![]()
又![]()
![]()
![]() 为公共角,
为公共角,
![]()
![]() ,即
,即![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.



 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
【题目】 “六一”前夕质监部门从某超市经销的儿童玩具、童车和童装中共抽查了300件儿童用品,以下是根据抽查结果绘制出的不完整的统计表和扇形图;
类别 | 儿童玩具 | 童车 | 童装 |
抽查件数 | 90 |

请根据上述统计表和扇形提供的信息,完成下列问题:
(1)分别补全上述统计表和统计图;
(2)已知所抽查的儿童玩具、童车、童装的合格率分别为90%、88%、80%,若从该超市的这三类儿童用品中随机购买一件,买到合格品的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,7个腰长为1的等腰直角三角形(Rt△B1AA1,Rt△B2A1A2,Rt△B3A2A3…)有一条腰在同一条直线上,设△A1B2C1的面积为S1,△A2B3C2的面积为S2,△A3B4C3的面积为S3,则阴影部分的面积是______ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD∥BC,AB⊥BC,AB=3.点E为射线 BC上一个动点,连接AE,将△ABE沿AE折叠,点B落在点B′处,过点B′作AD的垂线,分别交AD,BC于点M,N.当点B′为线段MN的三等分点时,BE的长为__________ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与x轴交于点A(3,0),与y轴交于点B,抛物线
与x轴交于点A(3,0),与y轴交于点B,抛物线![]() 经过点A,B.
经过点A,B.
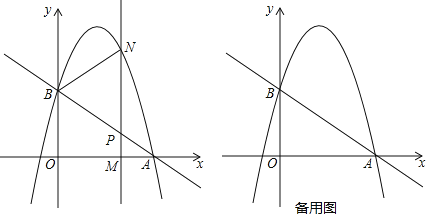
(1)求点B的坐标和抛物线的解析式;
(2)设点M(m,0)为线段OA上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N.
①求PN的最大值;
②若以B,P,N为顶点的三角形与△APM相似,请直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学在“书香校园”活动中,为了解学生的读书情况,学校抽样调查了部分同学在一周内的阅读时间,绘制如下统计图.根据图中信息,解答下列问题:
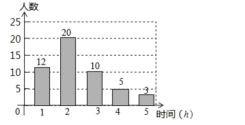
(1)被抽查学生阅读时间的中位数为____h,平均数为_____h;
(2)若该校共有2000名学生,请你估算该校一周内阅读时间不少于3h的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,抛物线y=ax2+bx-2与x轴交于点A(-3,0)、B(1,0),与y轴交于点C.
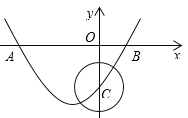
(1)求抛物线的函数表达式.
(2)在抛物线上是否存在点D,使得△ABD的面积等于△ABC的面积的![]() 倍?若存在,求出点D的坐标;若不存在,请说明理由.
倍?若存在,求出点D的坐标;若不存在,请说明理由.
(3)若点E是以点C为圆心且1为半径的圆上的动点,点F是AE的中点,请直接写出线段OF的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2﹣4ax+3a.
(1)若a=1,则函数y的最小值为_______.
(2)当1≤x≤4时,y的最大值是4,则a的值为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com